离散数学：数理逻辑、集合论

发表于 更新于 分类于

distribute

（一）

image-20240526213759080

上面的蕴含等值式和等价等值式

A->B

“¬”、“∧”、“∨”

p→q 等价于 ¬p∨q

A↔️B 等价于 (A→B) ∧（B←A）

德摩根

分配率

归谬论

假言易位

等值演算法的步骤，分配率化到最后，然后观察

对偶

并换成交 T换成F

范式

析取范式 合取范式

  • 主析取范式：给定的析取范式，每一个合取式都是极小项，m010 ∨ m011 ∨ m100

    极小项: 每个命题变元都要出现，也就是一直交，交到最小

    极小项析取（并），极大项合取（交）

    极小项是各个命题变元交得来的。极大项是各个命题变元并来的

  • 主析取范式和主合取范式互补。

  • 如果出现极小项并一个简单Q或者R，扩充成1∧Q∧1 也就是 (P∨¬P)∧Q∧(R∨¬R)

完备集

只要出现∧或者∨中的任何一个，再加¬，就是完备集

命题逻辑的推理理论

前提引入和结论 ==附加前提（结论是蕴含）== ==归谬法==

  • 附加律 ==A 推出 A∨B==

  • 化简律 ==A∧B 推出 A==

  • 假言推理 ==(A→B)∧A 推出 B== A真，B一定真

  • 拒取式 ==(A→B) ∧ ¬B 推出 ¬A== B是假的 A也一定是假的

  • 析取三段论 ==(A∨B)∧¬B 推出 A== B是假的 A并B真 A肯定真

  • 假言三段论 ==(A→B)∧(B→C) 推出 A→C== 传递

  • 等价三段论 等价的传递性

  • 构造性二难 ==(A→B) ∧ (C→D) ∧ (A∨C) 推出 B∨D==

  • 破坏性二难附加律

  • 1 2 合取

谓词逻辑

把一句话改写成函数的形式，共同点

Fx x是素数 F1 1是素数 F2 2是素数

全称量词和存在量词

蕴含 合取（命题符号化的时候）

∀ ∃

合取 析取（消去量词的时候）

指导变元 辖域：约束出现 自由出现

辖域收缩：跟X没关系的，比如y 直接剥离出去

  • 量词分配律：

    全称量词对合取 存在量词对析取 这样才是等价

    否则 全称A ∨ 全称B → 全称A∨B

​ 存在A ∧ B → 存在A∧存在B

​ 个体域abc，代表三个实数，如果遇到x，y共同约束，先解决其中一个。此即为谓词公式的置换，能够求出谓词公式的真值

  • 前束范式 ：约束全在前面
    • 改写成前束范式：否定换到后面，多个量词指导变元相同，应该换元。如果之前是自由变元，后来又有了约束，那也一样要换元，以保持前面的自由度
    • 两种情况需要进行换名：
      • 当辖域不同的重名变量存在时，需要使用不同的名字
      • 当 约束变元 和 自由变元 命名发生冲突时，最好将 约束变元 及其 指导变元 进行改名
    • 当进行量词合并或者拆分的时候，一定不要想当然，要根据合并或者拆分的规则和定理进行。
    • 先看量词的辖域，看约束变元和自由变元

推理理论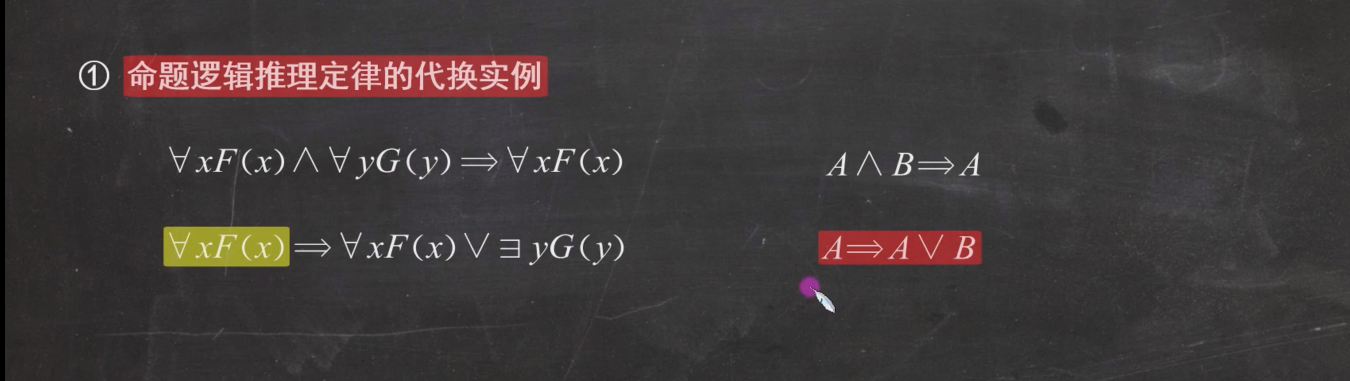image-20240528012816323

image-20240528101406789

  • 全称A∨全称B → 全称 (A∨B)

​ 存在 (A∧B) → 存在A∧存在B

​ 全称（A→B) 推出 全称A→全称B

​ 存在A→存在B

逆向 附加 归谬;引入错误结论，推出与前提矛盾的点

证明中间把量词去掉，也就是代入，最后再加上量词

image-20240528013613611

引入量词要注意加上对应规则

集合论

包含关系：子集包含于某个集合

属于关系：元素属于某个集合

对称差：A并B-A交B

差运算：A-B 属于A不属于B

A的绝对补集 ~A = E-A

有穷集计数：

多个并：奇+偶- 每个加数都是交集

A并B并C

非A交非B交非C

二者互补

A-B并C = A-B 交 A-C

A-B交C = A-B 并 A-C

A-B = A交~B

A是B的子集, A-B等于🈳

对称差：交换性 结合性

A 对称差 🈳 =A

A 对称差 A = 🈳

A和~A的对称差为 E

AB对称差等于AC对称差 推出 B=C

证明集合恒等式 可以额外添加一个A

二元关系

笛卡尔积，有序对，AB笛卡尔积为mn个元素，不满足交换律和结合律，满足分配率

非空，元素是有序对 为二元关系，空集是个二元关系

AXB 的子集 叫做 A到B的二元关系 ，特别的AXA为A上的二元关系，所以A的二元关系为 2^n^^2^ 个

空关系🈳

全域关系 AXA EA 全集

恒等关系 <x,x> IA {<1,1><2,2><3,3>}

关系矩阵 按照数对的顺序填1或0 用MR 表示

关系图 恒等关系就是环，自己画一个圈，剩下的画有向边

关系运算 domR ranR domain and range

R的定义域和值域的并集 为 域 fldR=domR 并 ranR

domR有序对的第一元素构成的集合

ranR有序对的第二元素构成的集合

image-20240528151530508

F⭕️G G对F的右复合 F中有3,3和6,2 G中有2,3 那么F⭕️G为 6,3 G⭕️F为2,3

关系性质和闭包

自反，对称，闭包

R在A上 自反 R，对于A中每个元素都有 11 22 33 的恒等关系 主对角线为1 有环

​ 反自反 R，对于A中每个元素都没有 11 22 33 的恒等关系 主对角线为0 没环

对称 任两个元素组合都有其 逆关系 有xy必有yx 对称矩阵。如果两点有边，只能是双向

反对称 任意两个元素的组合都没有其 逆关系 如果两点有边，只能是单向

传递：任意 的xy属于R yz属于R 能推出xz属于R 如果x到y y到z 那么x到z肯定有边

先给出全域关系

反对称，关于对称轴对称过去的值相反 1对称过去是0, 0对称过去是1

传递性图解

闭包

R是A上的关系，R的xx闭包是A上的关系R’

R’⊂R

rst 分别对应自反对称传递闭包

自反闭包：把R补全，然后不要漏掉原来的元素

等价关系

R是自反对称且传递的关系

image-20240528192239902

自反性，代入x.x 得x,x∈T 运用了

传递性，代入xy，

对称性，代入y，x，其实就是反着代了一下，原式子还是不变的

划分：：不能有空集，且各个集合之间不能有交集

偏序关系

自反 反对称 传递

树 上 的 小于等于关系 , 集合上的包含关系 , 非 *0 00* 自然数之间的整除关系 , 都是常见的偏序关系 ;

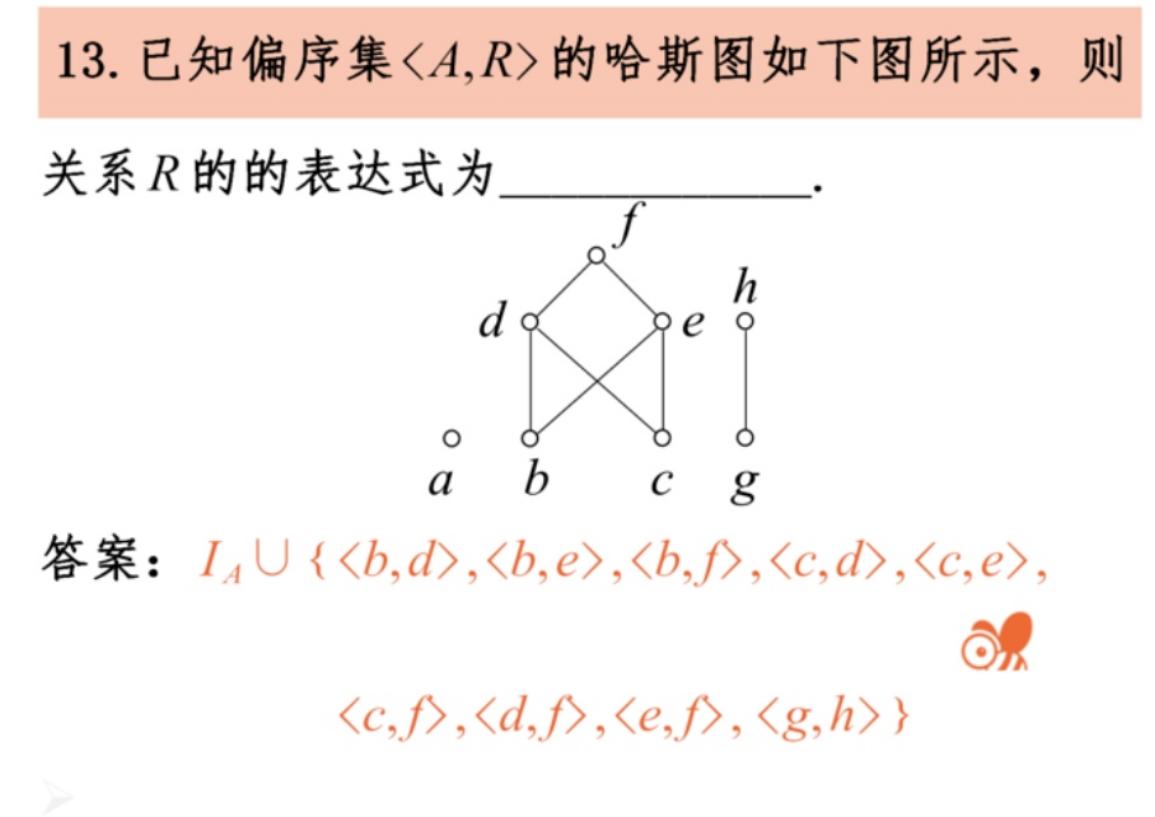
哈斯图

没关系的画在一排上，有关系的画成层次结构

第一部：排点的层数

第二部：把有关系的点连接起来，

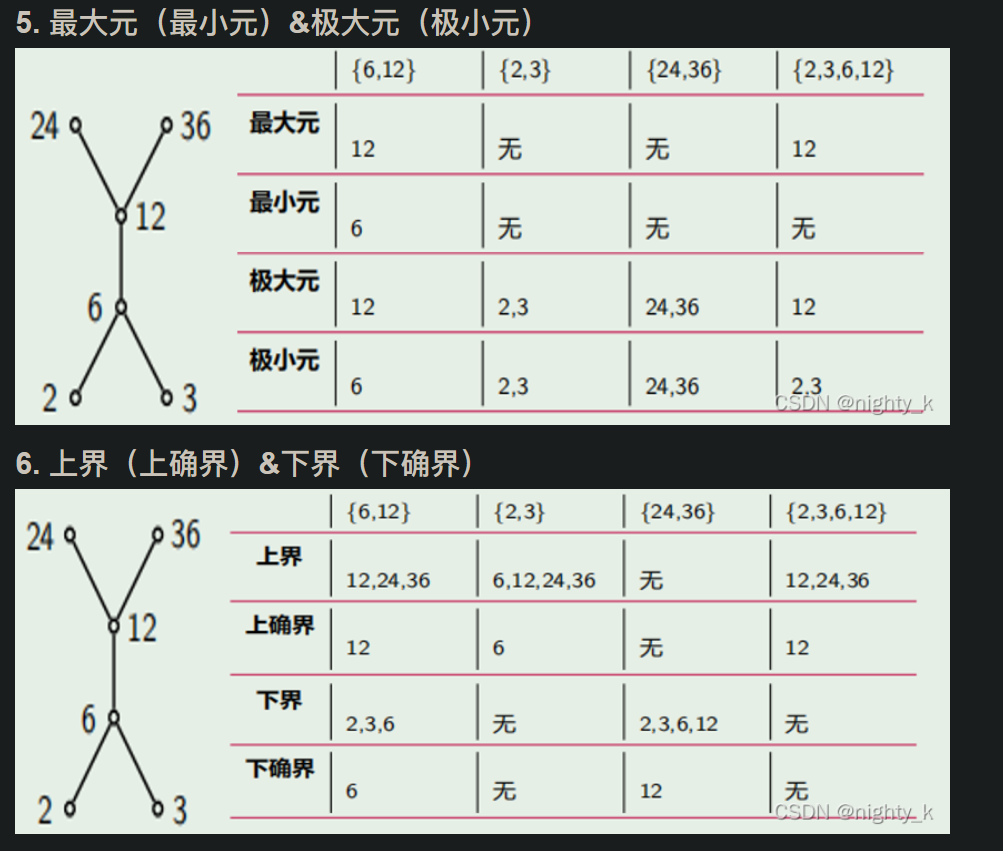
image-20240528203053473

在哈斯图中的位置：只有有层次结构的才可以比较，23不可比（最大最小）

​ 极大极小，就是没有最大最小值时候的权宜之计,把不可比的全扔上去

上界：只要有大于等于这些元素就可以

上确界：最小上界 下确界：最大下界 （必须可比）

上下界是针对全体集合来说的，下界

image-20240528214006655

射： 单射 必须一一对应 dom < ran

​ 满射 值域都取到了 dom > ran

​ 双射 dom = ran

f AtoB

g BtoC

f⭕️g AtoC

fx⭕️gx = g（fx）本质就是复合运输