数的运算 CPU 指令系统
数和运算
无符号和有符号数
无符号数
寄存器位数就等于无符号数的位数
有符号数
符号位+数值位
机器数是机器中的表示方法，真值就是真实的值。比如真值为+1，机器数就是00001(四位二进制+符号位)
原码表示法
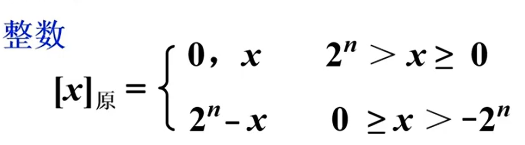
7的原码 0111 真值共3位
-5的原码先取反5即101，再加2^3^ 1101，n是数据位数
本质是带符号的绝对值，符号被数字化，小数如下：
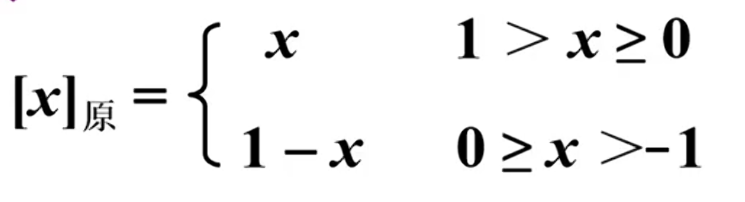
问题：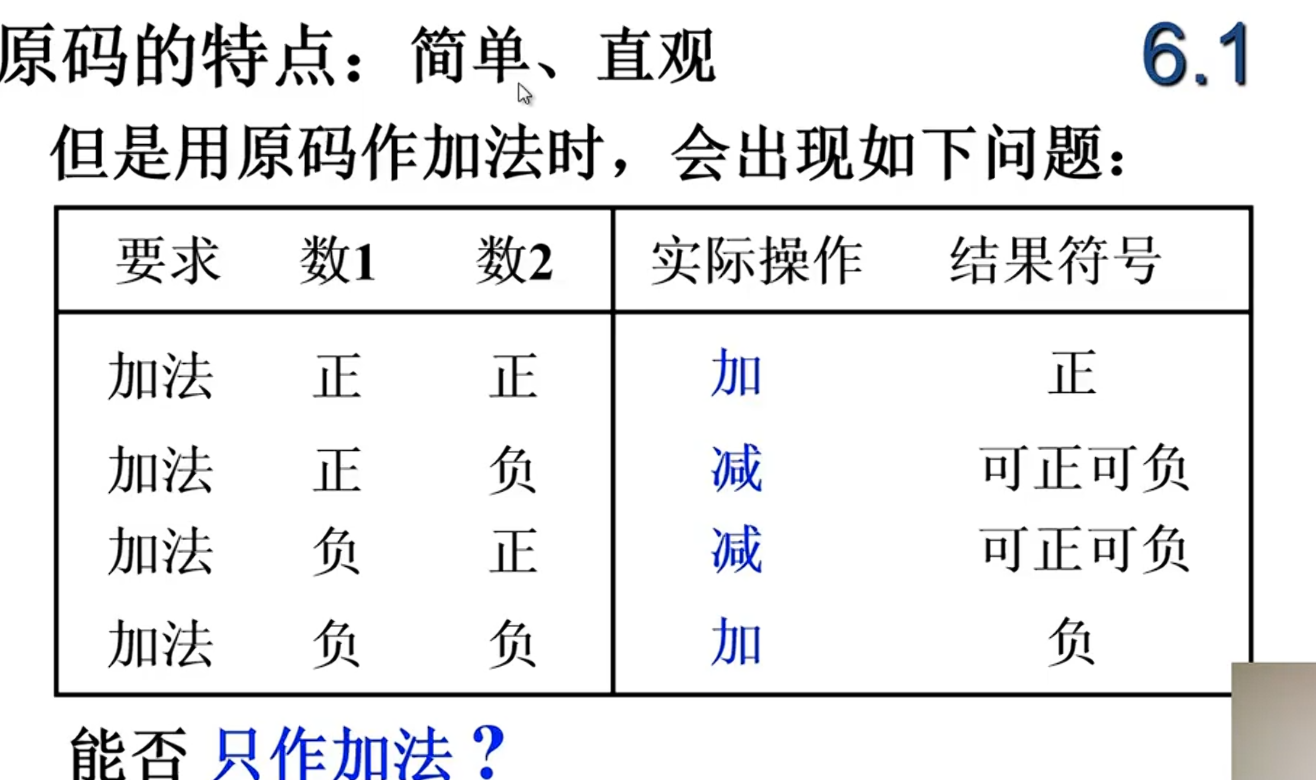
能否找到一个与负数等价的正数，代替这个负数，使的加这个负数就等于加她的等价正数？
补码
补的概念
加负数等于加他的补数
两个互为补数的数加模仍然互为补数
所以正数的补数就是他本身
但是此时有一个问题，没法区分是正还是负，所以再加一个符号位，用32为模
-1011+100000 = 1 0101
1011+ 100000 = 0 0101
-1011加一个模变成0101，但区分不出来，所以再加一个模，变成1 0101 能区分了
==定义：==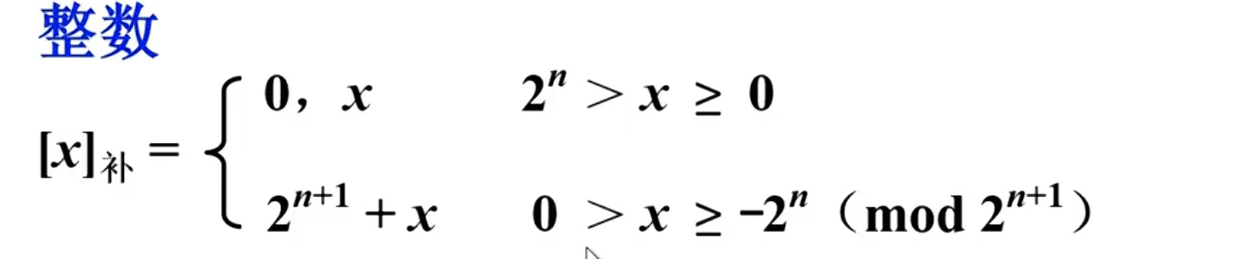 
x表示真值。n是整数的位数，踢去符号位。
原码表示2+（-2）:0,0000010+1,0000010=1,0000100 得-4，显然不对
如果用反码表示，还是不对，但是离正确结果很近了，只需要加1
所以-2应该是11111111的写法
整数的补码：0只有1种表示形式，所以补码能多表示一个-8
小数的补码：0只有1种表示形式，所以补码能多表示一个-1
移码
只是符号位和补码不同
定点数和浮点数
定点数
约定小数点位置
记住一点：补码就是能比原码多表示一个数，用四位举例，原码1111=-0.875，变成补码就是1001了，此时还剩下一个1000没有对应的，那就让他对应-1好了。四位的整数同理，原码只能表示-7到7，因为由正零和负零，如果变成补码就能多表示一个，就让多出来的1000表示-8
浮点数
为什么
相差太大需要很长的机器字长
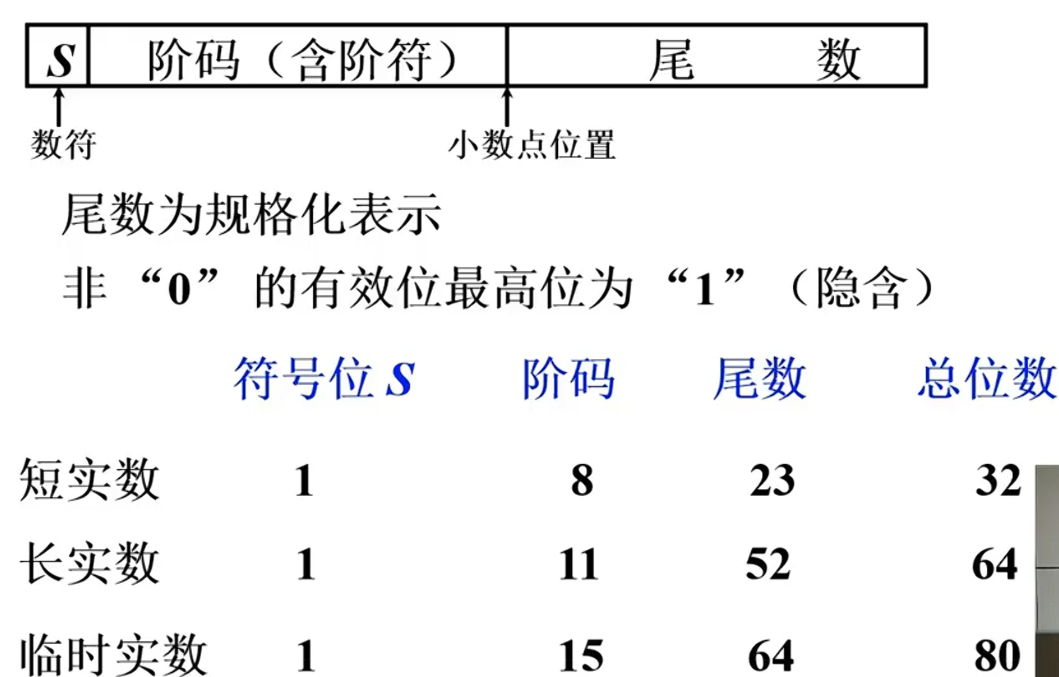
表示方法
定点数(尾数) + 阶码
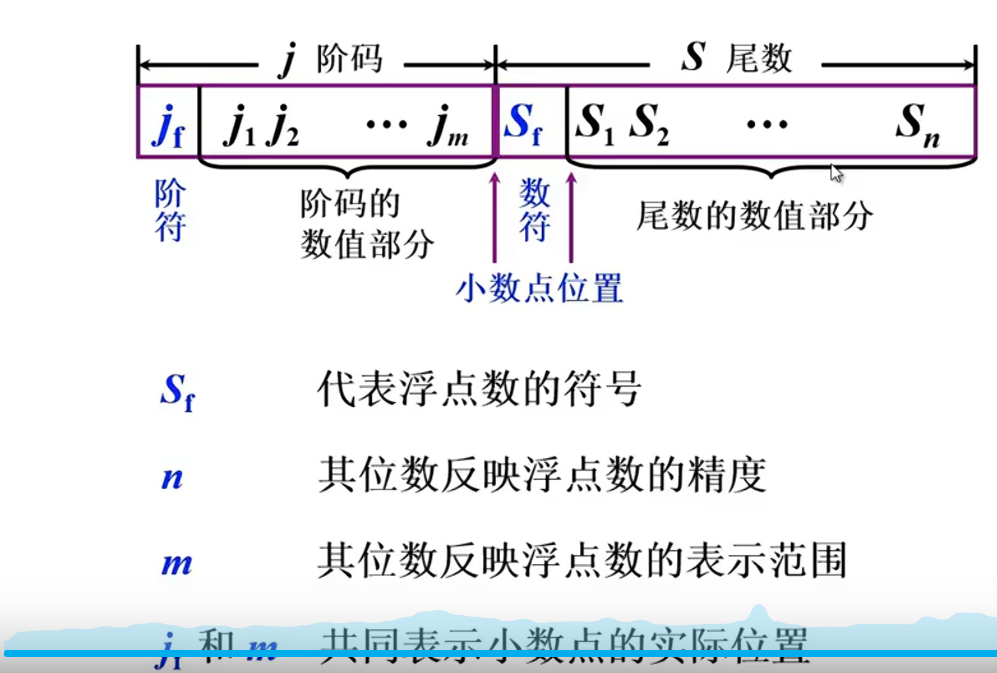
表示范围
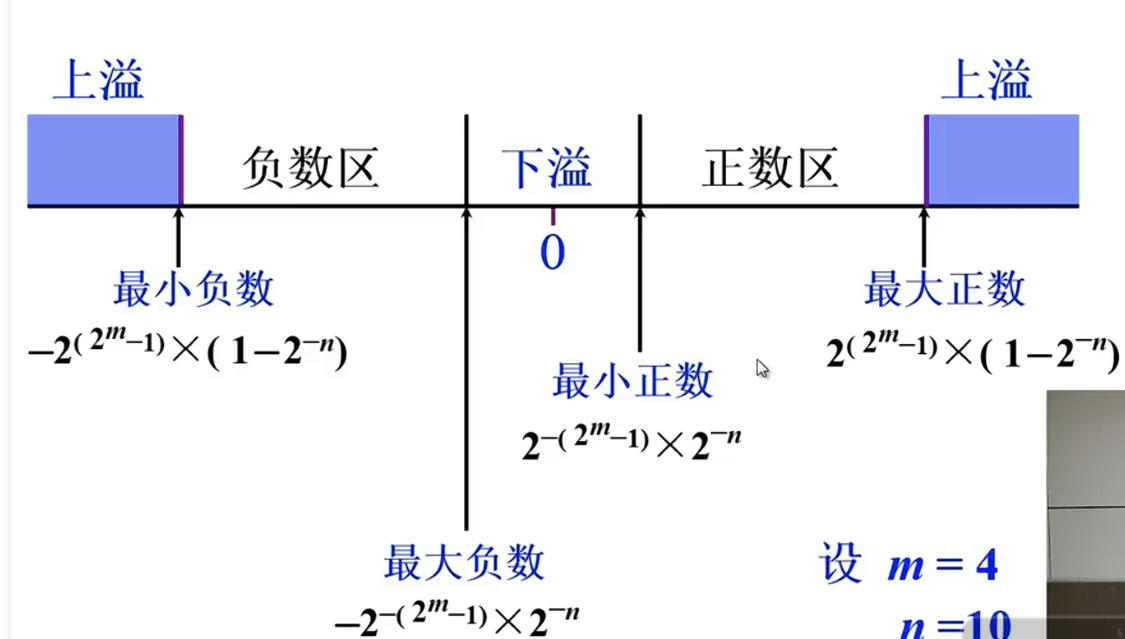
下溢：0，上溢：错误
表示±3w的十进制数，阶符数符各一位，要搞清楚，尾数就是0.xxxxx，绝对值永远是小于1的，那么要想让N表示±3w，r^j^ 必须是3w+ 所以j阶码长度占4位，保证最大精度，剩下的全是尾数
规格化
为什么规格化？
r=2时，尾数如果最高位是0，就不算最简，通过阶码的变动仍然能让其变成更简
r=4时，尾数如果最高位是00，通过阶码变动仍然能让其变得更加简单
二进制定点：整数在最后，小数在第一位后面
二进制浮点：规格化形式，
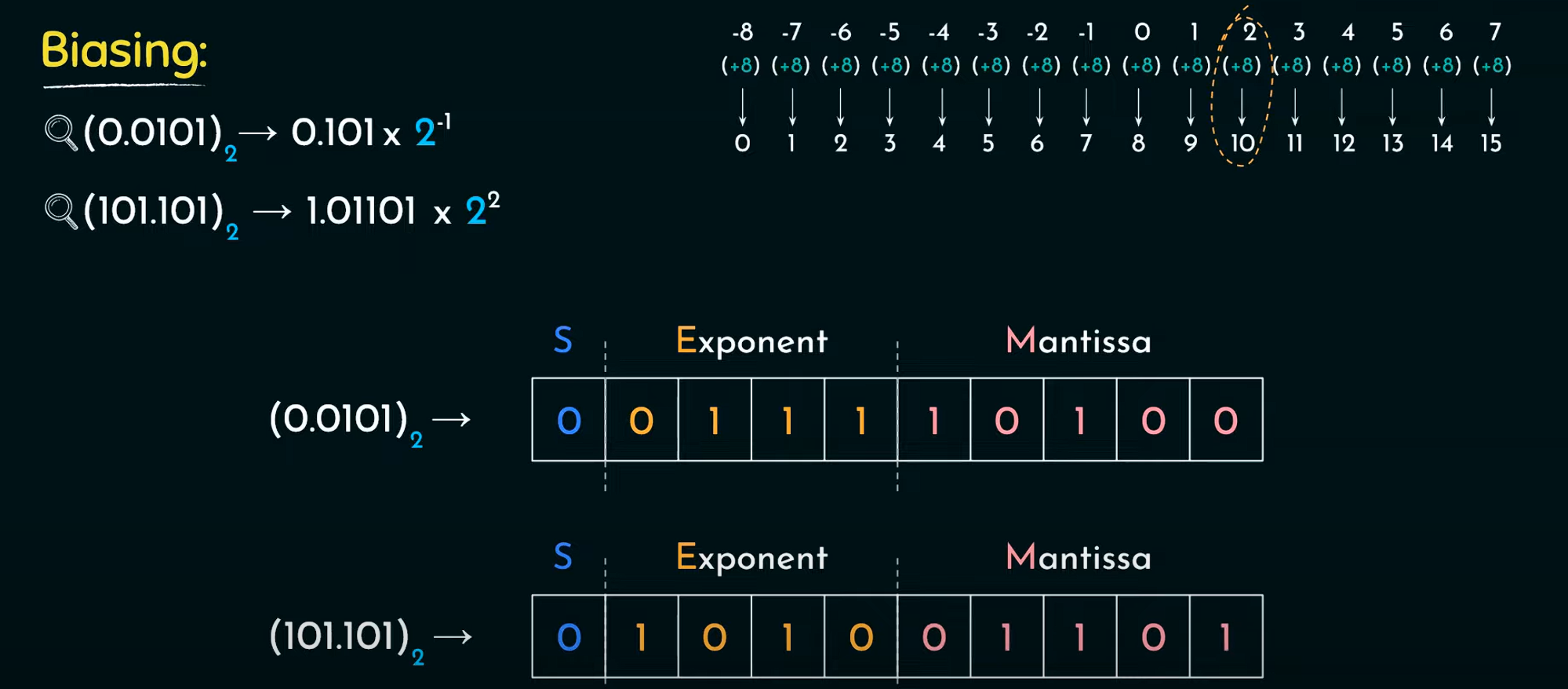
Explicit
符号位+ Exponent（阶码） +尾数
机器0
r=2,所以把1隐含掉
8位移码：0~128~255 分别对应真值-128~0~127
7位补码尾数：补码0只有一个，多出来的一个就变成-1
正数：2^7^ ~ 1-2^7^
负数：-1 ~ -2^7^
定点运算
定点移位运算
算数移位
移位：数据相对于小数点移动
左移：绝对值变大
右移：绝对值变小
与加减配合实现加减乘除
算数移位规则
符号位不变
| 码制 | 添补代码 | |
|---|---|---|
| 正数 | 原反补 | 0 |
| 负数 | 原码 | 0 |
| 反码 | 1 | |
| ==补码== | 左移，右侧空出来添0 | |
| ==补码== | 右移，左侧空出来添1 |
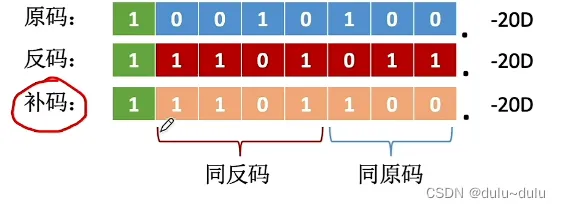
对于原码（包括正数的原反补和负数的原码）来说，1是有意义的，左移丢1，误差很大，相当于丢了权重最大的一位，补了个0。右移丢1，误差较小，丢了权重最小的一位。
对于负数的补码来说，根据补码的规律，最右边的“1”的右边的数与原码一致，左边的数与反码相同，所以左移丢1对数据没有影响，右移丢1，误差较小
对于负数的反码来说，1是没有意义的，0才有意义，所以丢1对数据没有影响。
反码加1变成补码，加1会导致进位，最右边的1就是进位的最终结果，补码这部分是100的原因：原来是这部分是100，取反以后变成011，加1必然导致进位变成100，这部分就跟原码一样了
-26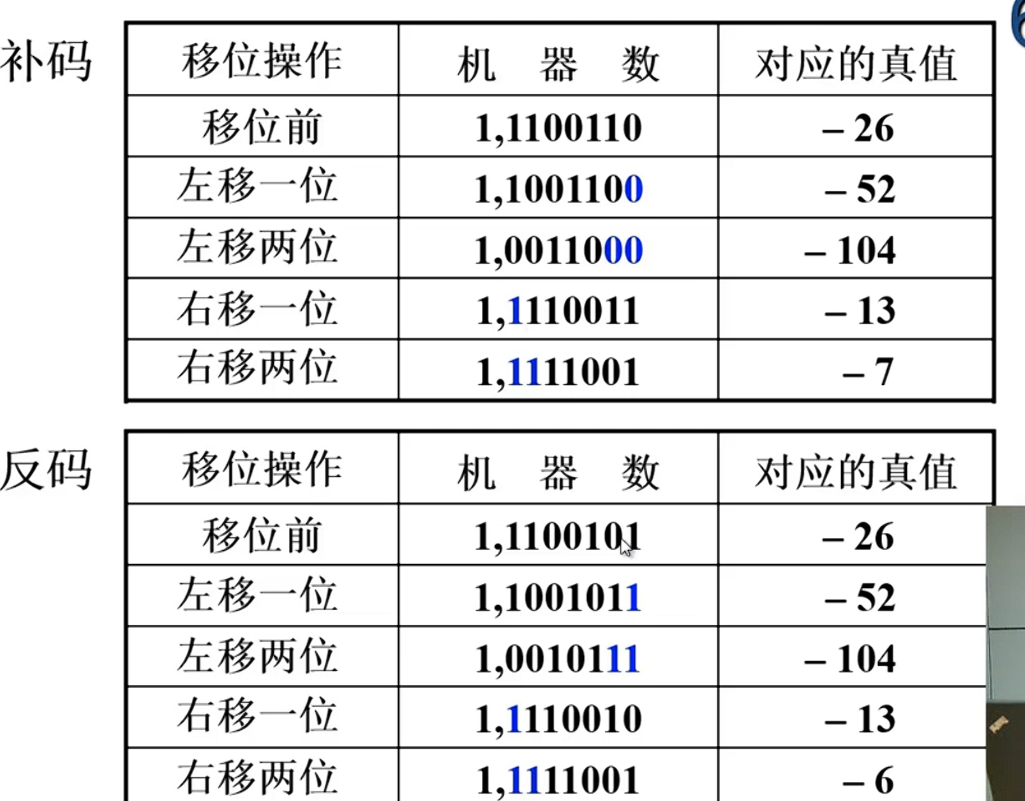
逻辑移位
把整个数看成一个无符号数，右移，高位补0低位舍弃，左移高位舍弃低位补0
循环移位
顾名思义
定点加减法
补码加减法公式
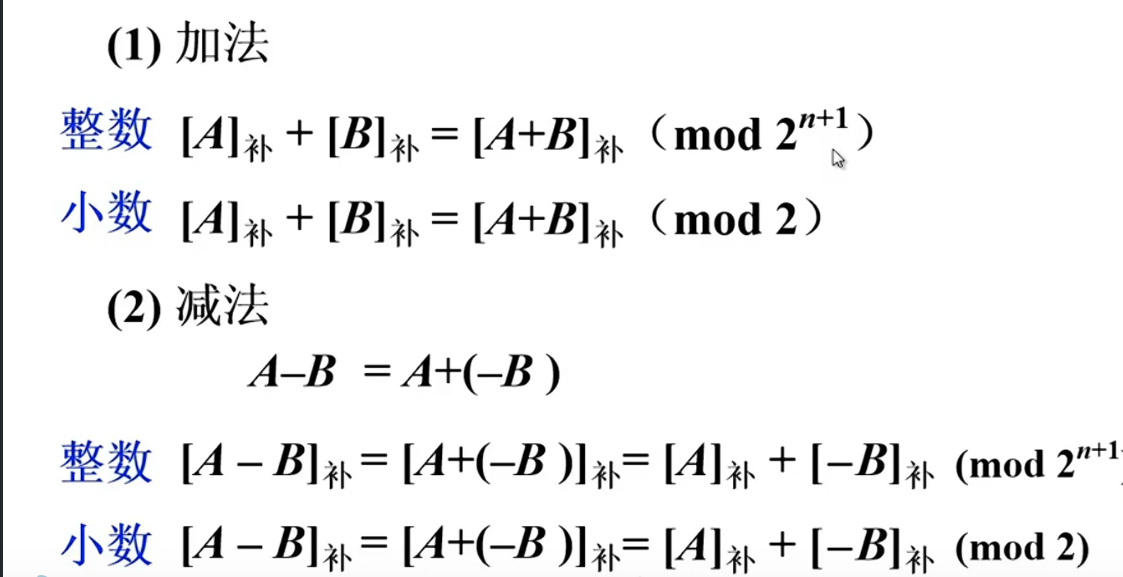
补码 负数跟正数 遵循模32规则，所以能进行加减
5-3⇔5+负三补码，此时算出来的补码就是一个正数，正数可以理所当然参与运算，并且是每一位都可以，
溢出？
一位符号位：两个操作数符号相同，结果符号与原来不同
最高有效位进位⊕符号位进位 = 1
两位符号位：
两个符号位异或
正数加正数：
如00，1111➕00，1000，此时的运算结果就为01，0111。
很明显，这发生了正溢出，因为在数值位只有4位，能表示的最大数值为1111，而运算结果显然超出了该范围，于是产生了像符号位的进位，造成上溢出。
负数加负数：
如11，1111➕11，1000，此时的运算结果就为11，0111。
显然，这没有发生了溢出，其原因是在负数补码中，高位的1相当于原码的0，于是如果两个操作数的数值位最高位都是1的话，是一定不会引起操作数溢出的，与正数两个最高位为0相加，不会发生溢出是一样的。如果，有其中一个为0的话，如果次高位传来进位，依旧可以保证对符号位的进位，也就是保证符号位不会发生变化，从而避免了溢出。
如果最高位为0就要小心溢出
低位必须产生进位，低位不进位肯定溢出
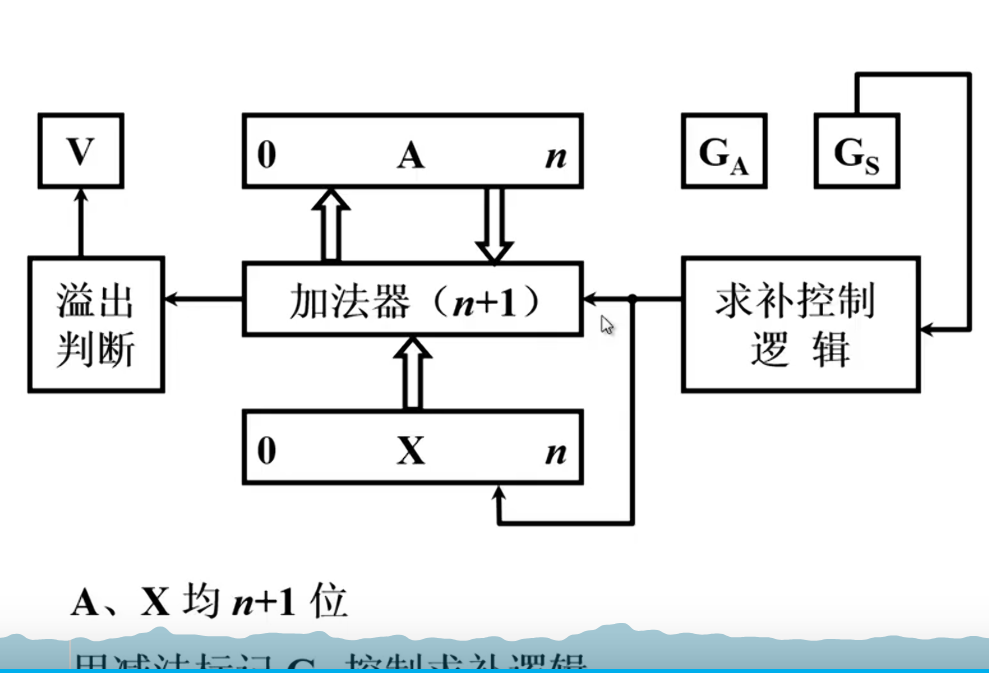
定点乘除法
原码一位乘：先加后右移，加4次移4次
看最后一位，1加的是原数，0不加
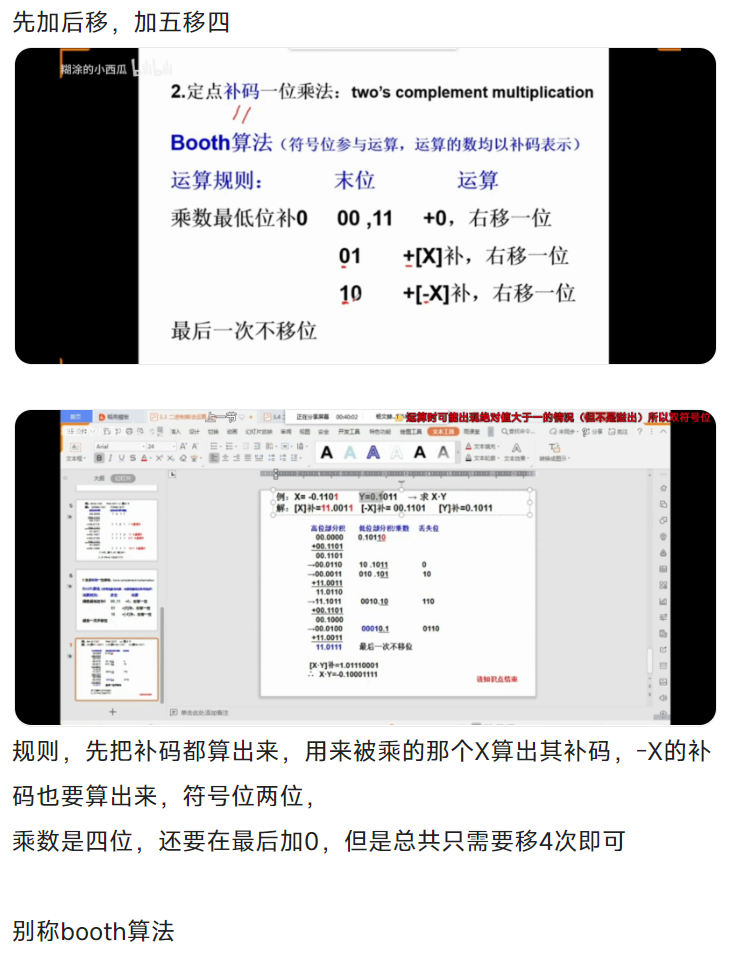
补码一位乘：先加后右移，加5次移4次
看最后两位，01加X补码，10加(-X)补码，11和00不加
原码定点除：先加后左移，加4次移4次
先加(-X)补码，差值正上1，加(-X)补码得到新差值；差值负上0，加X补码得到新差值，直到商有效位够4位
补码定点除：先看同号否，同号r为x-y，异号r为x+y，
ry同号上1，同时左移，加-y补得到新r，ry异号上0，同时左移，加y补得到新r，再比较同号否
加，上商，左移
上了四次商之后，同时左移，商末位恒为1
加4移5
原码定点一位乘
补码定点一位乘（Booth）
原码定点除法
补码定点除法
加4移5
浮点运算
浮点加减法
S1:对阶
大阶对小阶，大阶左移丢1，如果是正数的话就是数据错误所以小对大
求阶差
小阶对大阶，小阶右移丢1影响较小 尾数右移1位，阶码加1.
S2:尾数求和
对阶移位完的尾数进行求和，按照定点补码加减法规则进行求和
S3:尾数规格化
r=2 尾数绝对值0.5~1
r=4 0.25~1
-1/2要进行左规
左规 相当于乘2
当尾数出现00.0𝑥𝑥⋯𝑥或11.1𝑥𝑥⋯𝑥时，尾数左移，阶码减1，直到数符(正负号)和第一有效数位不同
右规 相当于除2
尾数右移，阶码加1，直到数符(正负号)和第一有效数位不同
尾数溢出(>1)的时候需要右规
S4:舍入
对阶和右规过程中，可能会出现尾数末位丢1的情况，影响精度，考虑舍入。简单截断可以
1)0舍1入：即在尾数右移时，被移去的最高数值位为0，则舍去;被移去的最高数值位为1，则在尾数的末位加1。这样做可能会使尾数又溢出，此时需再做一次右规。
2)末位恒置“1”：尾数右移时，不论丢掉的最高数值位是“1”还是“O”，都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种可能。
S5:溢出判断
与定点数加减法一样，浮点数加减运算最后一步也需判断溢出。
在浮点数规格化中已指出，当尾数之和（差）出现01.×××或10.xxx时，并不表示溢出，只能将此数右规后，再根据阶码来判断浮点数运算结果是否溢出。
浮点数的溢出与否是由阶码的符号决定的。以双符号位补码为例，当阶码的符号位出现“01”时，即阶码大于最大阶码时，表示上溢，进入中断处理;当阶码的符号位出现“10”时，即阶码小于最小阶码时，表示下溢，按机器零处理。实际上原理还是阶码符号位不同表示溢出，且真实符号位和高位符号位一致。
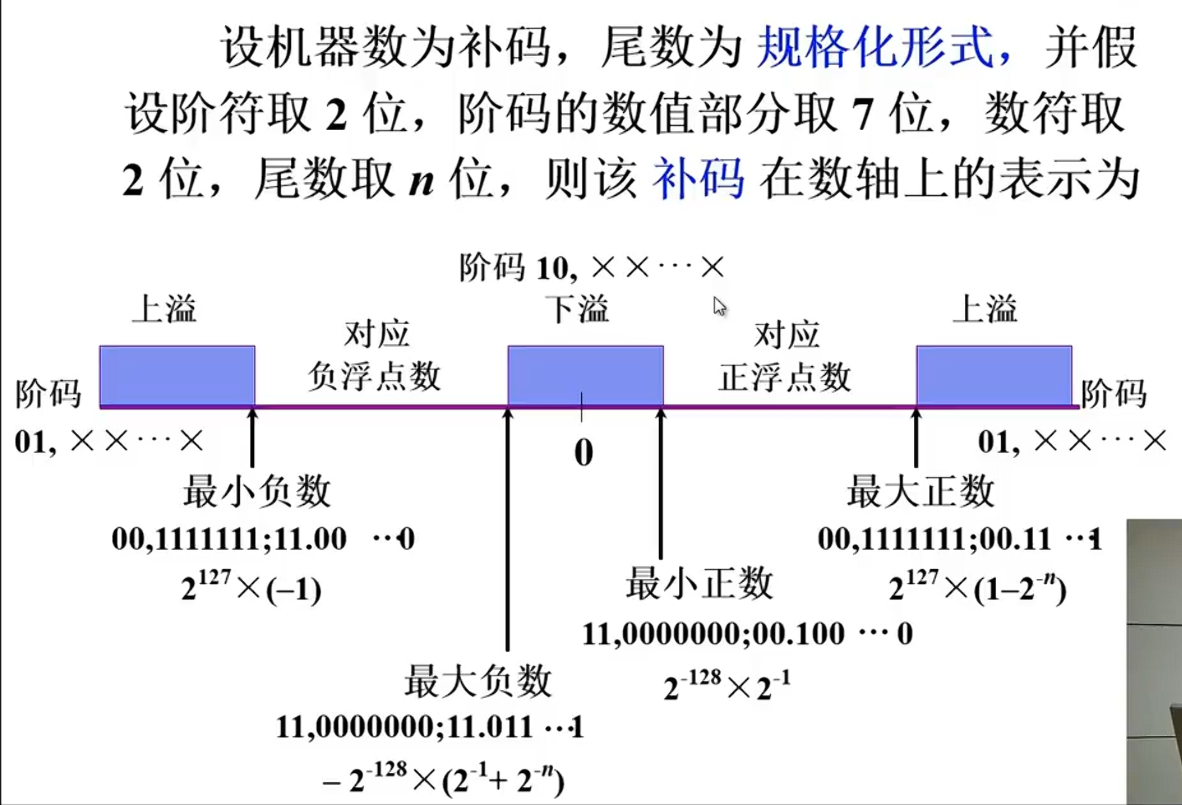
最大负数：11.1000…..0 表示-1/2但它不是规格化数，11.0111…..1,应该变小一点,减去2^-n^。尾数原来是-1/2，最后尾数变成-(1/2+2^-n^)
负数的补码应该是100000加到111111，越加越大，所以要从110000变成101111就要减去一个最小单位
误差分析
尾数溢出，右规丢1会引起误差
对阶，小对大，右移丢1会引起误差
ALU-算数逻辑单元
Arithmetic Logic Unit
ALU电路
组合逻辑电路 74181 控制端 CLA
需要寄存器保存结果
M=0，M=1 算数运算和逻辑运算
S3~S0 不同取值 可以做不同运算
快速进位
并行加法器
A和B两个数可以同时加进来，然后进行运算，四个位各自算各自的e
很多全加器接在一起
串行进位 Ripple Carry
Propagate & Generate
Pi = Ai⊕Bi , Gi = AiBi
Ci = AiBi + Ci-1(Ai⊕Bi)
=Gi + PiCi-1 ，C-1 = 0
Si = Ai⊕Bi⊕Ci
并行进位（超前进位） LookAhead Carry
Ci =Gi + PiCi-1 ，C-1 = 0
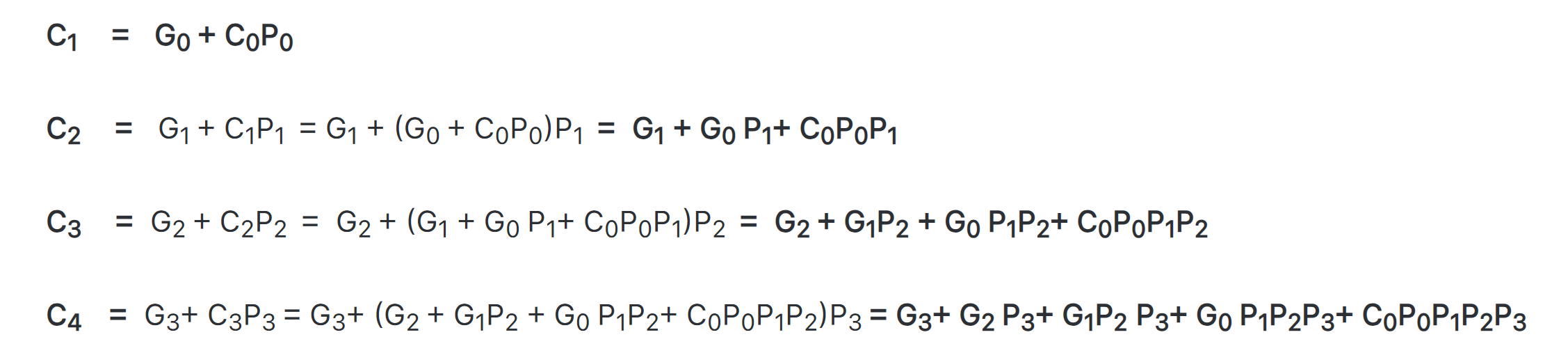
用电路复杂度换取速度
按照公式可以计算出C0到C3的结果
Si = Ai⊕Bi⊕Ci
单重分组跳跃进位链
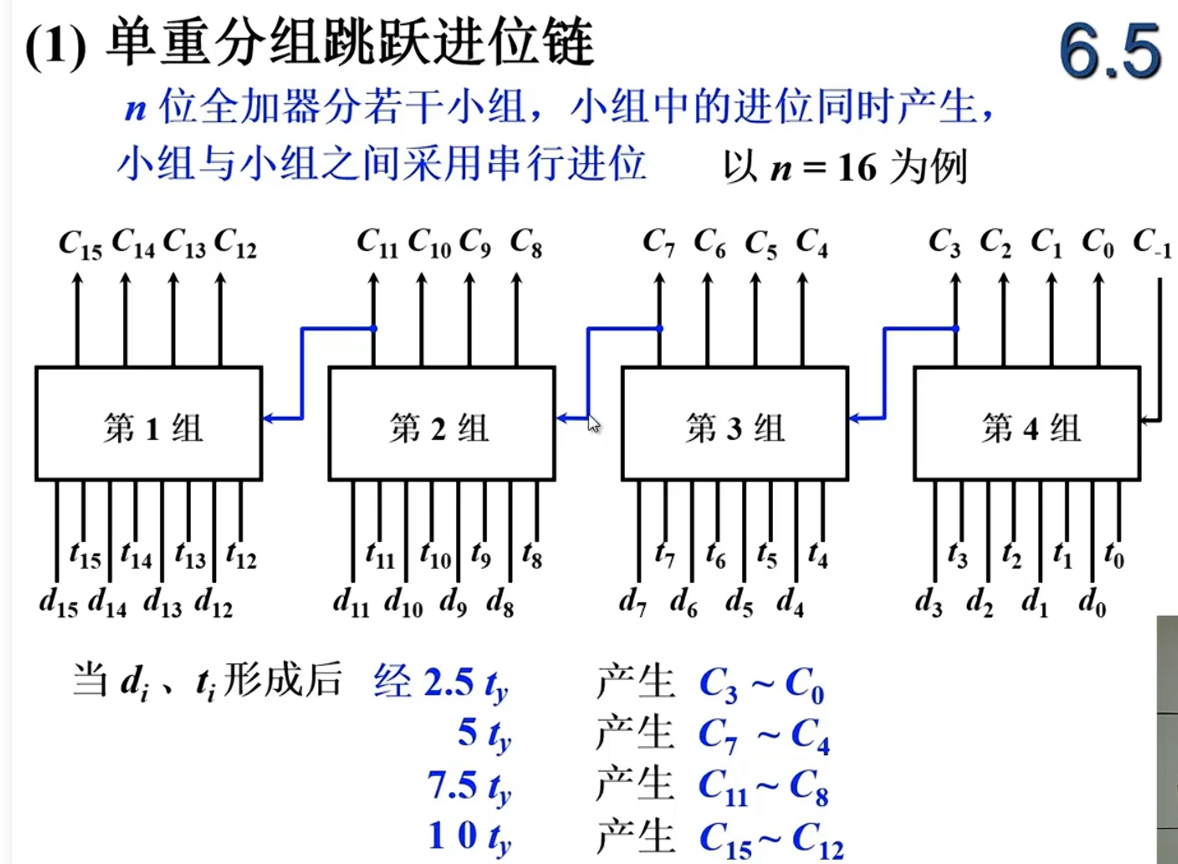
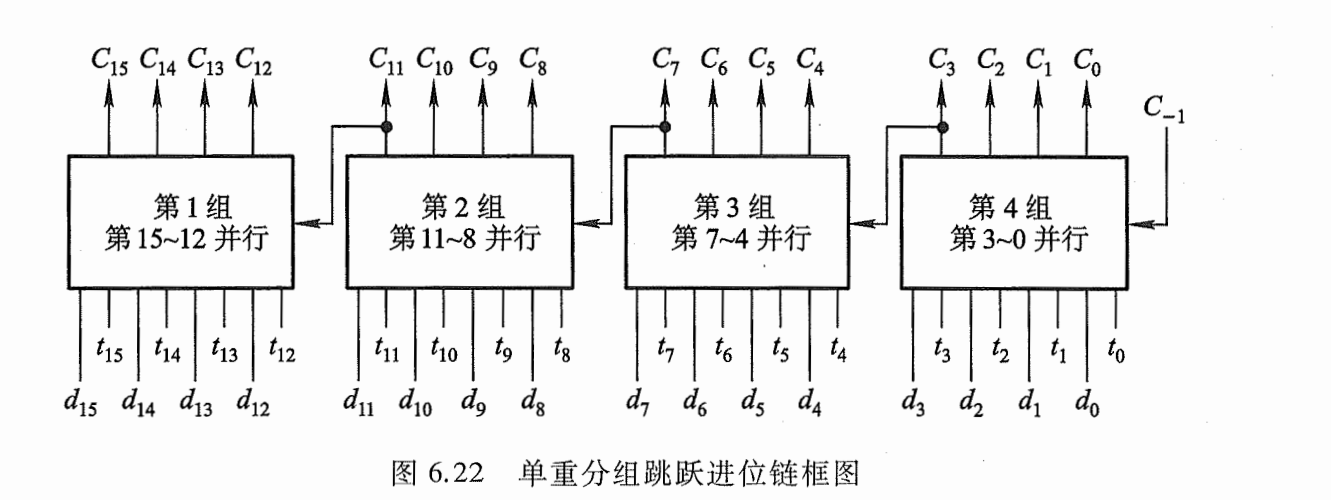
折中的办法，组内先行进位，组外采用串行进位，C0-C3同时产生
双重分组跳跃进位链
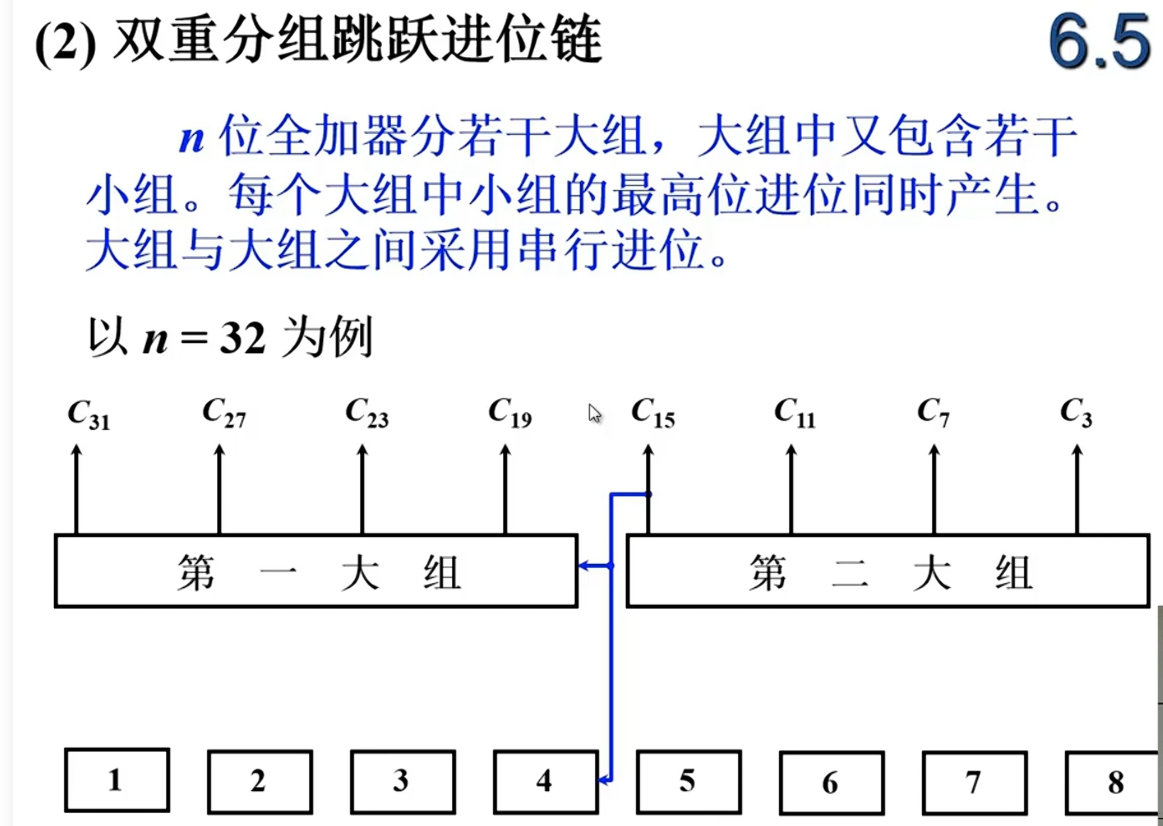
小组的最高位进位并行产生，大组之间采用串行
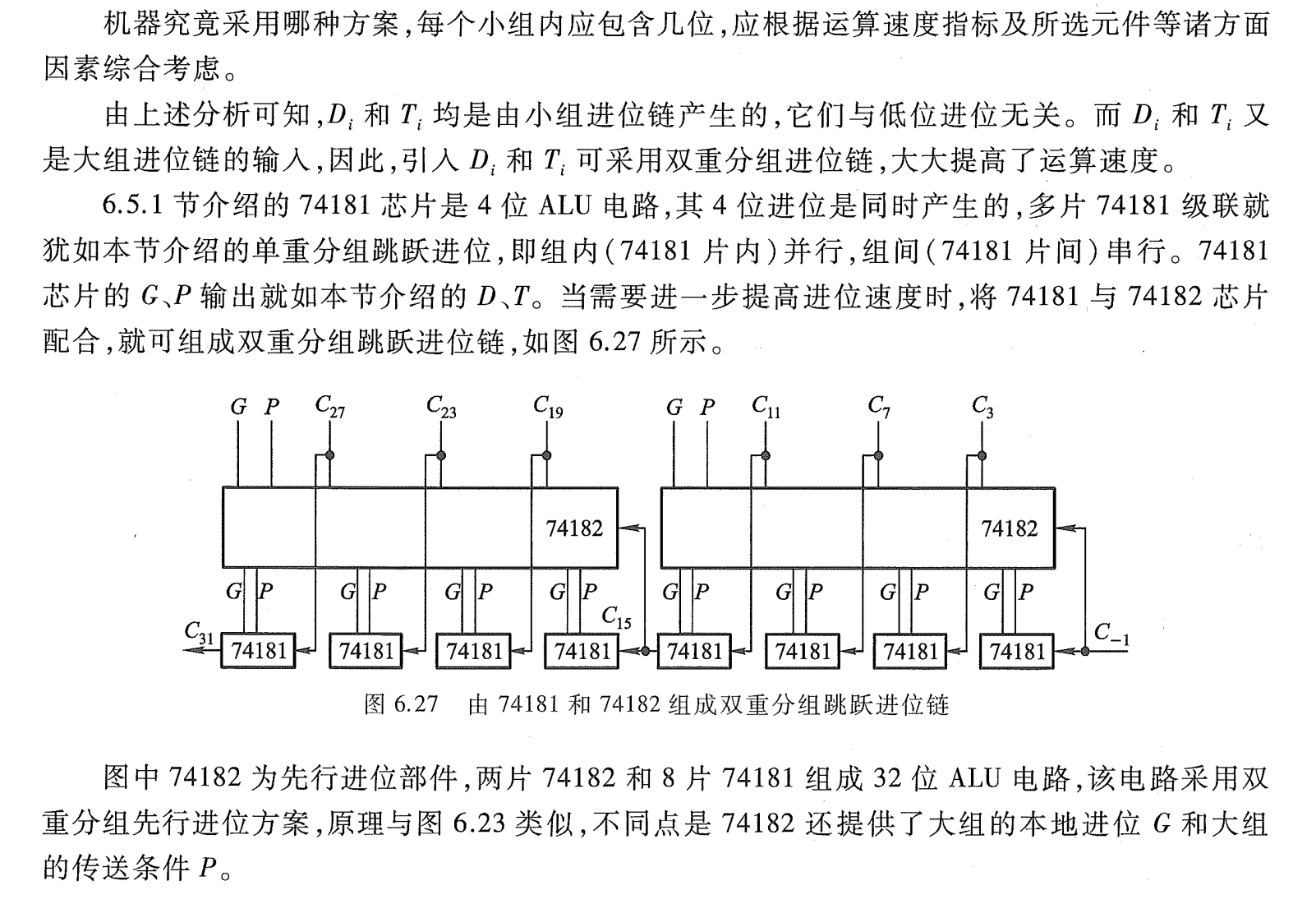
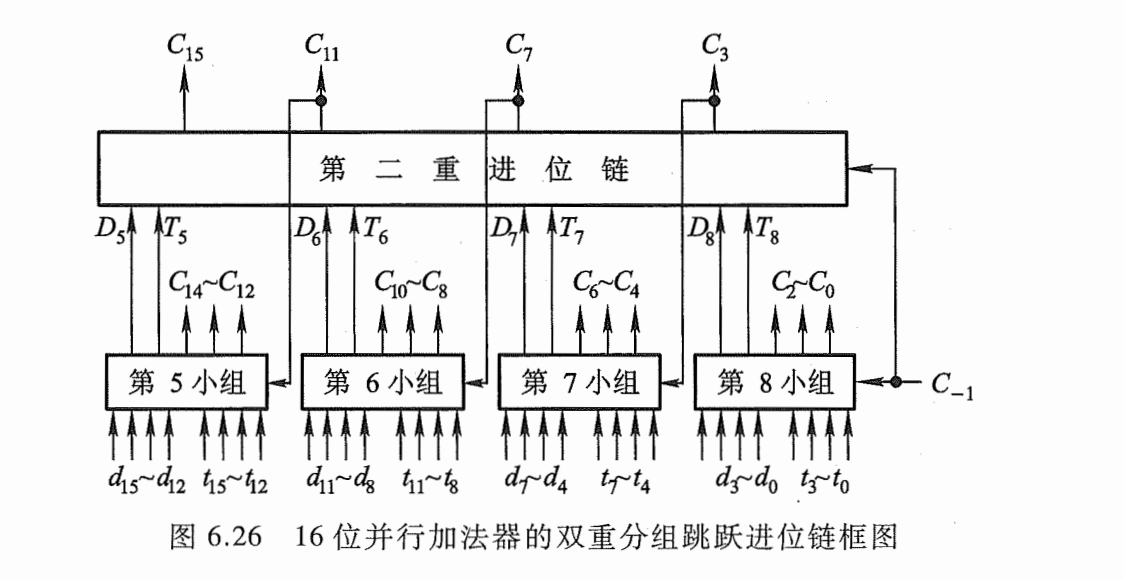
这种电路称为成组先行进位电路（BCLA)。利用这种4位的 BCLA电路及进位产生与传递电路和求和电路可以构成4位BCLA加法器。16位的两级先行进位加法器可由4个BCLA加法器和1个CLA电路构成，如图2.18所示。
这种方法可以扩展到多于两级的先行进位加法器，如用三级先行进位结构设计64位加法器这种加法器的优点是字长对加法时间影响甚小;缺点是造价较高。
指令系统
指令系统连接软件和硬件
机器指令
指令= 操作码+地址码
操作码长度可以固定，用于指令字长比较长的情况，也可以变化比如X86
为了使操作码扩展，可以让操作码的位数随地址码的减少而增加。
在设计扩展操作码指令格式时，必须注意以下两点:
不允许短码是长码的前缀，即短操作码不能与长操作码的前面部分的代码相同。
各指令的操作码一定不能重复。通常情况下，对使用频率较高的指令分配较短的操作码，对使用频率较低的指令分配较长的操作码，从而尽可能减少指令译码和分析的时间。
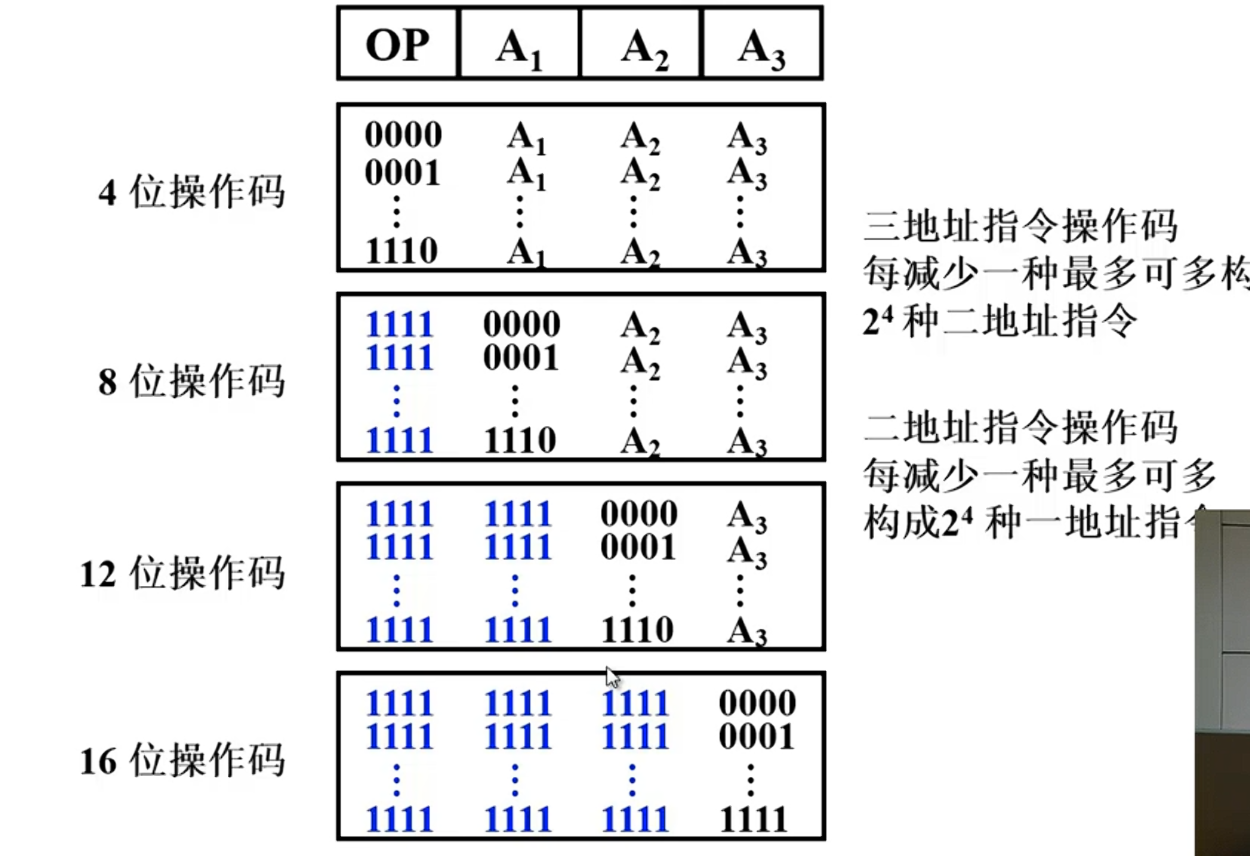
按照操作数地址码个数可以分为：
操作数地址码的长度一般是一样的,如果长度为8,寻址范围就是2^8^ 个.
零地址: OP
3)让(ACC)OP->(ACC) ACC自加
一地址: OP+A1
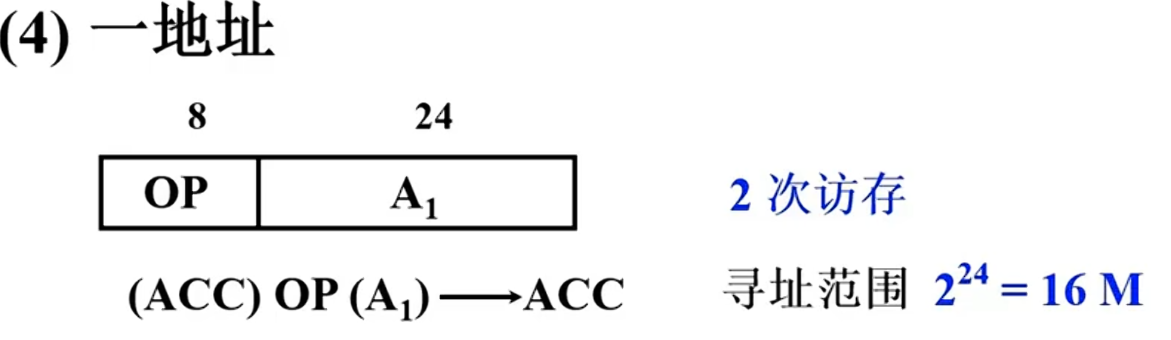
二地址: OP+A1+A2
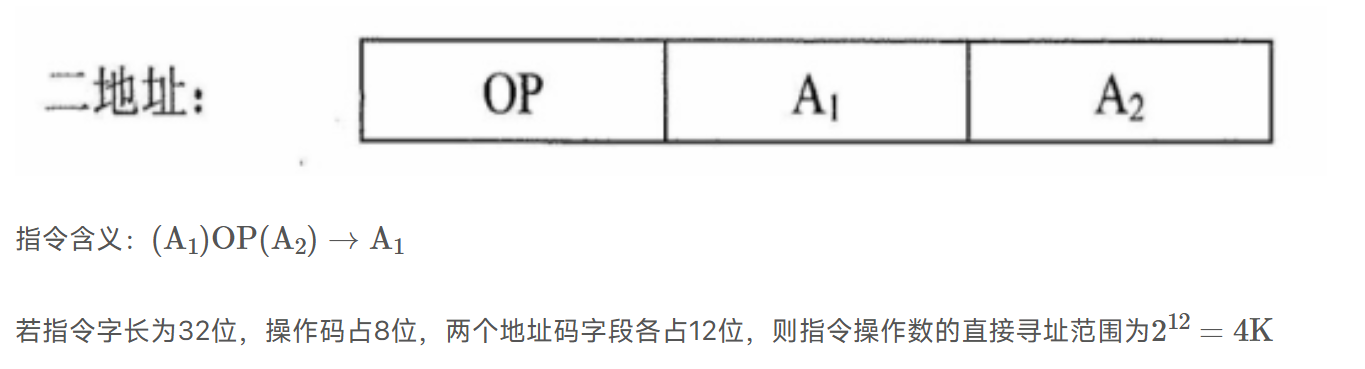
ACC代替A1/A2,
三地址:OP+A1+A2+A3(结果)
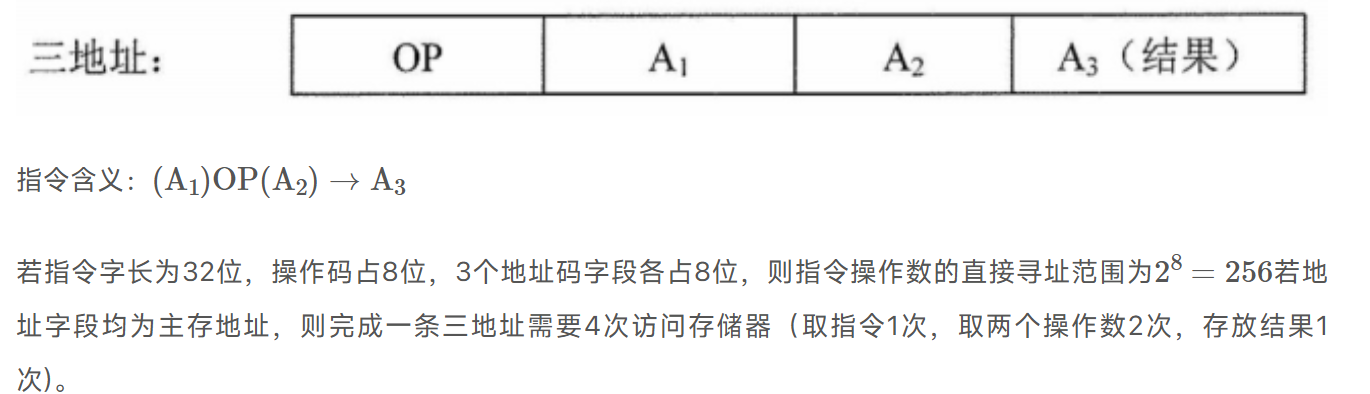
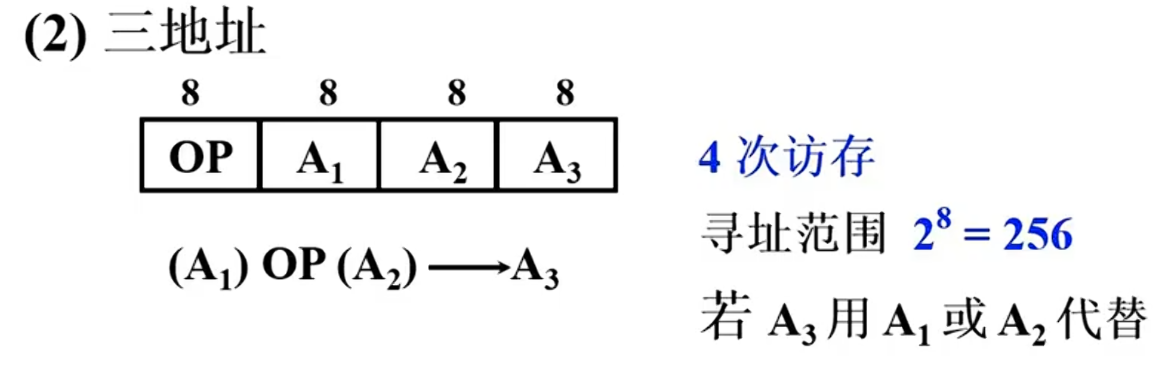
四地址: OP+A1+A2+A3(结果)+A4(下个地址)
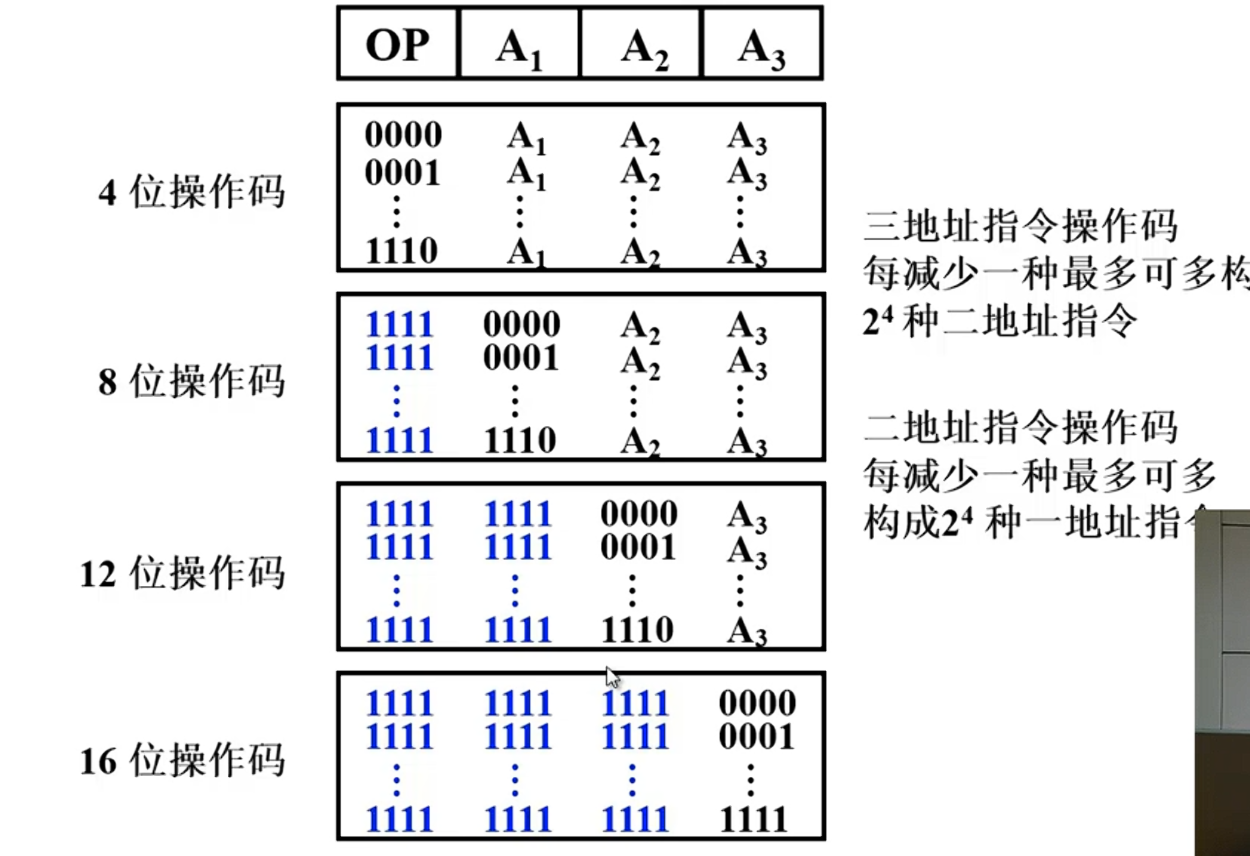
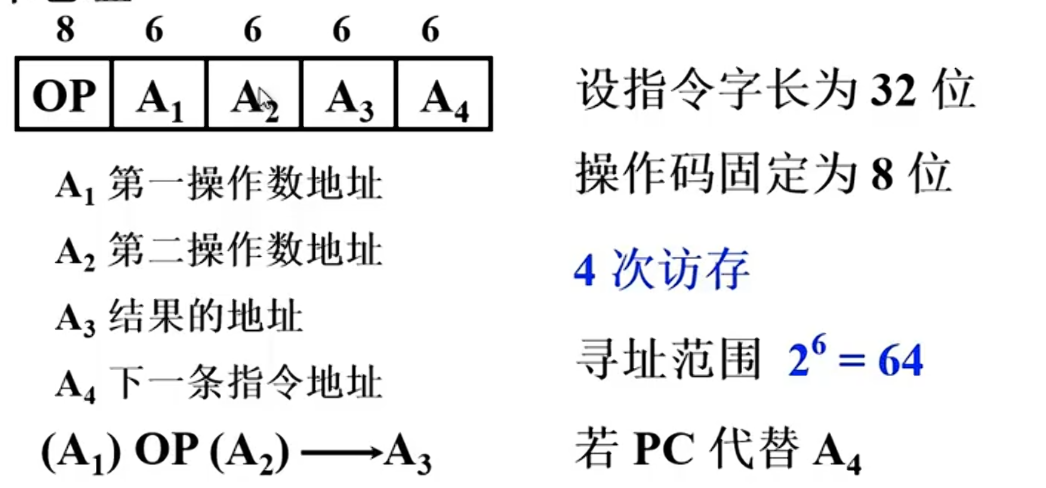
寻址范围从上到下逐渐降低
指令字长
指令长度和机器字长没有必然联系，指令长度等于机器字长 单子长指令，等于半个机器字长 半字长指令， 等于2个机器字长 双字长指令
指令长度相等，定长指令字，长度因功能而异，称为变长指令字结构，通常都是按照字节的倍数变化
总结
用硬件资源(ACC)代替指令字中的地址码字段：
- 扩大指令寻址范围（指令长度固定，地址码长度增加，能够操作的地址长度变多）
- 缩短指令字长（地址码长度不变，指令长度固定，但是地址码的个数变少，能够缩短整体的字长）
- 减少访存次数 ACC代替操作数，ACC代替结果，都能减少访存次数
指令的地址字段为寄存器：
- 指令执行阶段，可以不访存
操作数
操作数类型
地址：无符号整数
数字：定点数、浮点数、十进制数
字符：ASCII
逻辑数：逻辑运算
存放数据的方式
前提：按照字节编址每一个地址能存放一个字节
机器字长=CPU寄存器位数
存放一个机器字的存储单元，通常称为字存储单元，相应的单元地址称为字地址。而存放一字节的单元，称为字节存储单元，相应的地址称为字节地址。
编址方式是存储器地 址的组织方式，一般在设计处理器时就已经确定了。如果计算机中编址的最小单位是字存储单元，则该计算机称为按字编址的计算机。如果计算机中编址的最小单位是字节，则该 计算机称为按字节编址的计算机。一个机器字可以包含数字节，所以一个存储单元也可占用数个能够单独编址的字节地址。
高地址和低地址
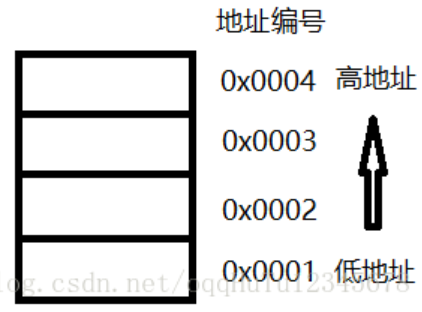
高字节和低字节
如int a=16777220，化为十六进制是0x 01 23 45 67，则04属于低字节，01属于高字节 是按照字节的位置区分的
大小端
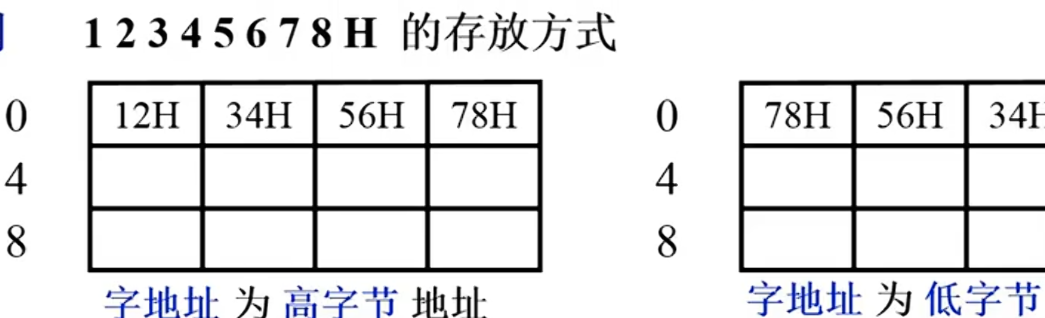
低字节存在高地址 大端，字地址在高字节的地址
| 地址 | 字节数据 |
|---|---|
| 0x0004 | 67 |
| 0x0003 | 45 |
| 0x0002 | 23 |
| 0x0001 | 01 |
低字节存在低地址 小端，字地址在低字节的地址
| 地址 | 字节数据 |
|---|---|
| 0x0004 | 01 |
| 0x0003 | 23 |
| 0x0002 | 45 |
| 0x0001 | 67 |
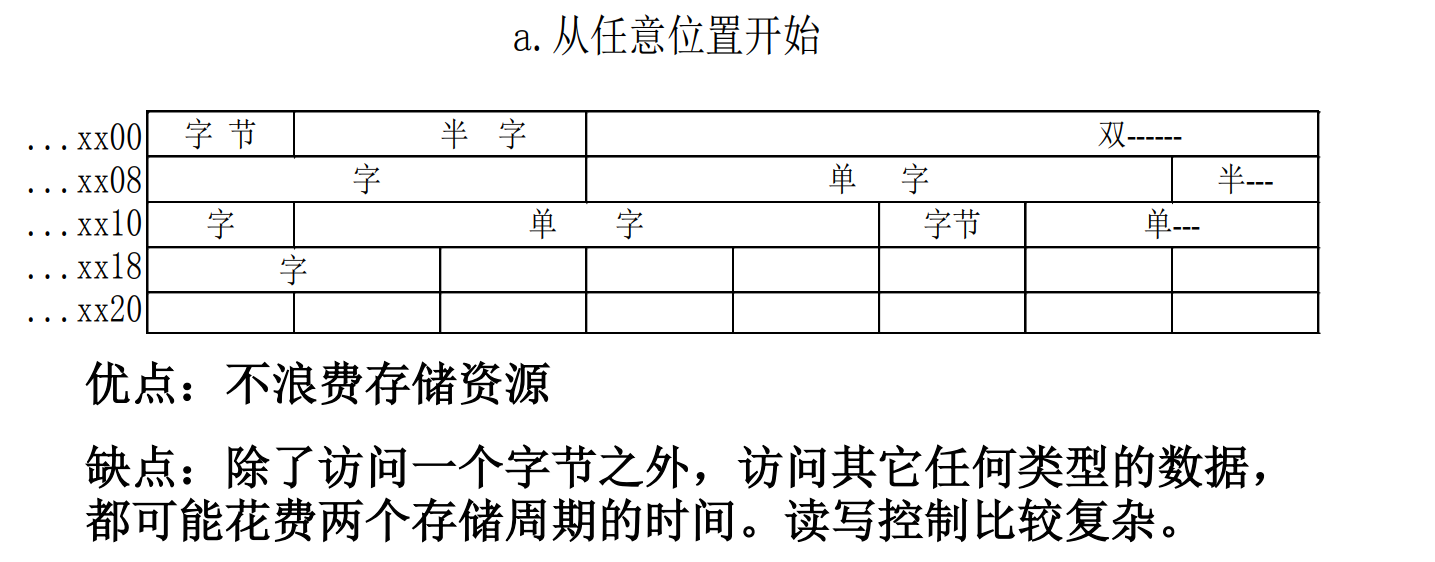
边界对准
按照字节编址，寻址时可以按照字，半字，字节。一个字是4个字节，字的地址就是4的倍数，半字的地址就是2的倍数，字节随便存。
存储字长：一个存储单元中存储的位数。要提高访存速度，就要在一个存储字长放入尽可能多且完整的的存储单位。
一个存储字中最多容纳4个地址，分别指向4个字节，半字只能存到字的开始或中间，全字必须独占一个存储单元。浪费了一些空间，但是不会造成同一个数据的分散，能够提高存取速度。
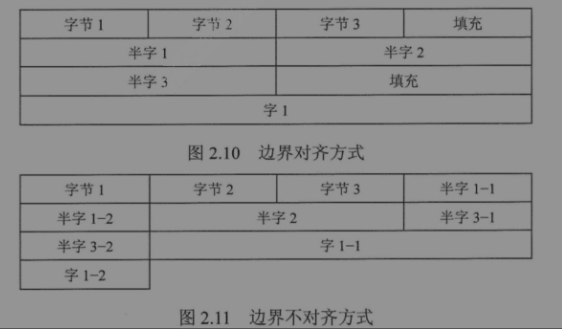
边界不对齐就会导致同一个字会存储到不同的存储单元中，导致访存次数增多，还要进行数据拼接等繁冗工作。
存储单元：每个存储单元 存放一串 二进制代码
存储单元 和 内存单元 是不一样的，内存单元是 存储单元的 子集。多个 内存单元 可以组成 一个 存储单元。
存储字（word）：存储单元中 二进制代码的组合
存储字长：存储单元中 二进制代码的 位数。
存储元：即存储一个二进制数的电子元件，每个存储元可以存储 1 bit。多个存储元 就可以 构成一个 内存单元。（由电容原理 制作出来的东西，因为电容可以 存储电荷呀 ~）
在这里 我们说的 存储字和存储字长，实际上 说的是 MDR 这个东西。
也就是这个 寄存器。它能存储 多大的数据。
所以我们也常说，存储字长 在 不同的硬件上 会 不一样。
操作类型
数据传送，算术和逻辑运算，移位操作，转移操作(JMP,CALL,RETturn,TRAP)，输入输出操作与外部IO交换数据
指令的寻址方式
确定本条指令的数据地址和下条待执行指令的地址。
可以通过指令寻址，也可以通过数据寻址。
操作码之后是寻址特征位，共采用的特征总和，分别编码表示即可。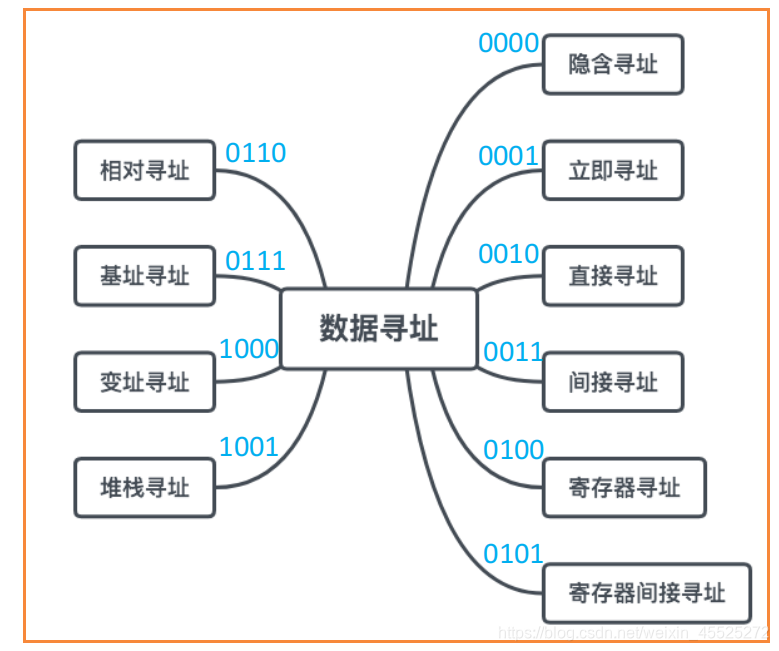
指令中的地址码字段并不代表操作数的真实地址，这种地址称为 形式地址形式地址 (A)。形式地址结合寻址方式，可以计算出操作数在存储器中的真实地址，这种地址称为 有效地址有效地址 （EA)。
注意，(A)表示地址为A的数值，A既可以是寄存器编号，也可以是内存地址。对应的(A)就是寄存器中的数值，或相应内存单元的数值。例如，EA=(A)意思是有效地址是地址A中的数值。
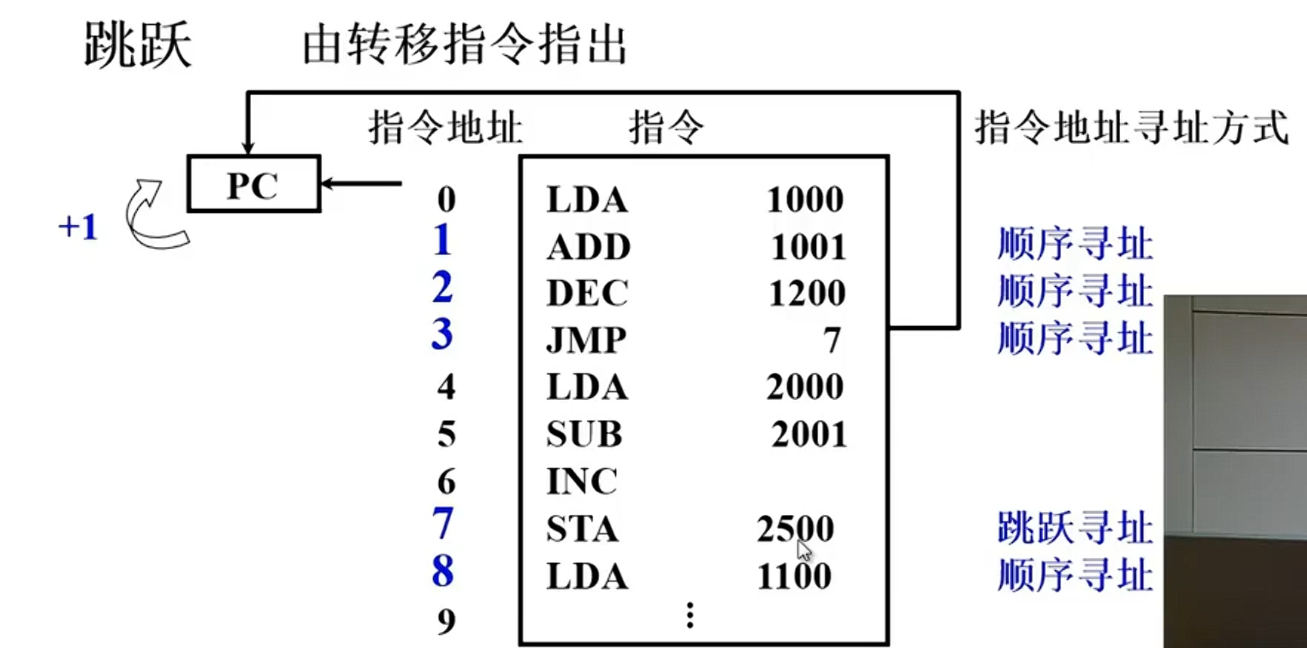
指令寻址方式
顺序
累加寄存器 ACC：它是一个同通用寄存器，其功能是：当 ALU 执行算术或逻辑运算时，为 ALU 提供一个工作区，ACC 暂时存放 ALU 运算的结果信息。显然，运算器中至少要有一个累加寄存器
PC寄存器用来存储指向下一条指令的地址，当执行一条指令时，首先需要根据PC中存放的指令地址，将指令由内存取到指令寄存器IR中，此过程称为“取指令”。与此同时，PC中的地址或自动加1或由转移指针给出下一条指令的地址。此后经过分析指令，执行指令。完成第一条指令的执行，而后根据PC取出第二条指令的地址，如此循环，执行每一条指令。
IR用来保存当前正在执行的一条指令。 当执行一条指令时，先把它从内存取到数据寄存器（DR，Data Register）中，然后再传送至IR。
GR 通用寄存器可用于传送和暂存数据，也可参与算术逻辑运算，并保存运算结果。除此之外，它们还各自具有一些特殊功能。通用寄存器的长度取决于机器字长，汇编语言程序员必须熟悉每个寄存器的一般用途和特殊用途，只有这样，才能在程序中做到正确、合理地使用它们。
PC+ “1” -> PC , 指令长度是4个字节，“1”就是4，指令长度是8个字节，“1”就是8，自动形成下一条指令的地址(这里是指指令的纵向长度)
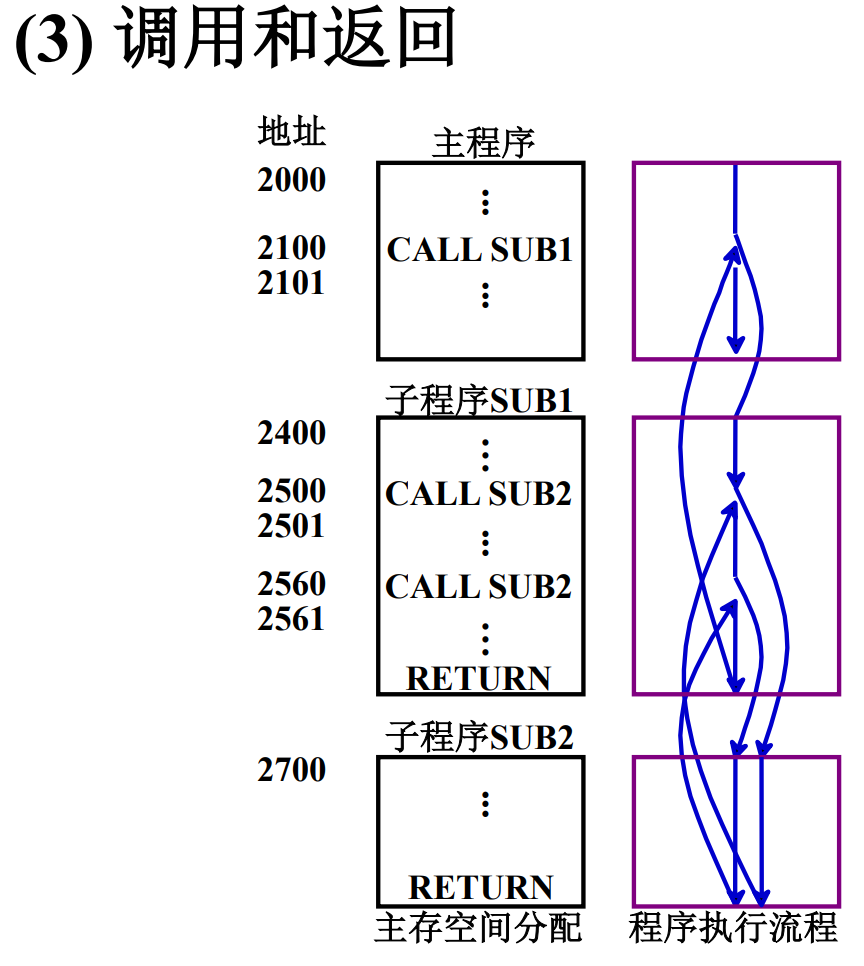
跳跃
通过转移类指令实现。所谓跳跃，是指下条指令的地址码不由程序计数器给出，而由本条指令给出下条指令地址的计算方式。注意，是否跳跃可能受到状态寄存器和操作数的控制，而跳跃到的地址分为绝对地址（由标记符直接得到)和相对地址（相对于当前指令地址的偏移量)，跳跃的结果是当前指令修改PC值，所以下一条指令仍然通过程序计数器（PC）给出。
数据寻址方式
EA地址存放了操作数
立即寻址
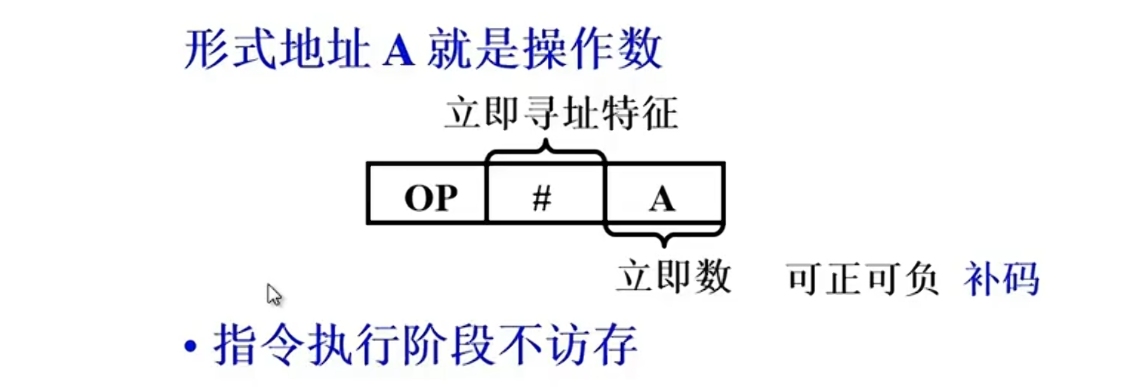
指令执行时间最短，但是A的位数限制了立即数的范围
直接寻址 EA=A
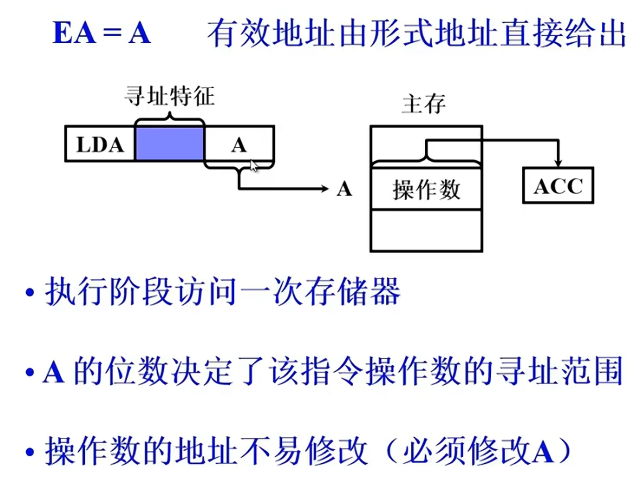
A就是地址，A的范围决定了寻址范围。
隐含寻址 A是一个操作数的地址
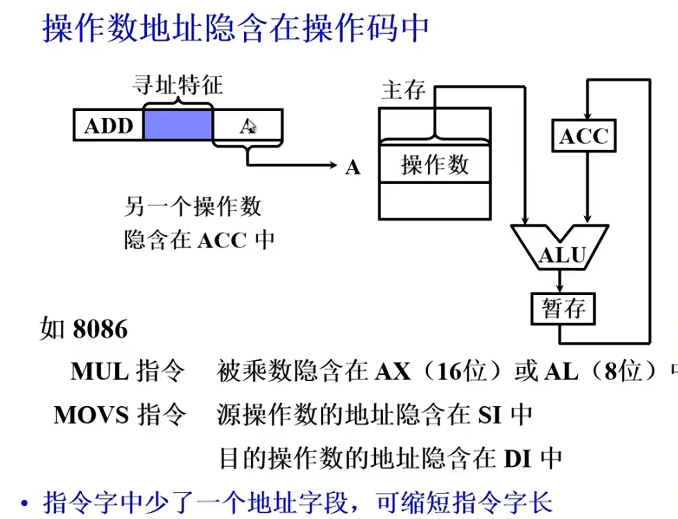
这里规定硬件ACC是第二操作数的地址，对于这种一地址指令，访存1次，零地址指令操作数是默认保存在一个寄存器中的。
间接寻址 指令的地址字段给出的形式地址不是操作数的真正地址，而是操作数有效地址所在的存储单元的地址，也就是操作数地址的地址，即 EA =(A) 还可以通过多次简介寻址 EA=((A))
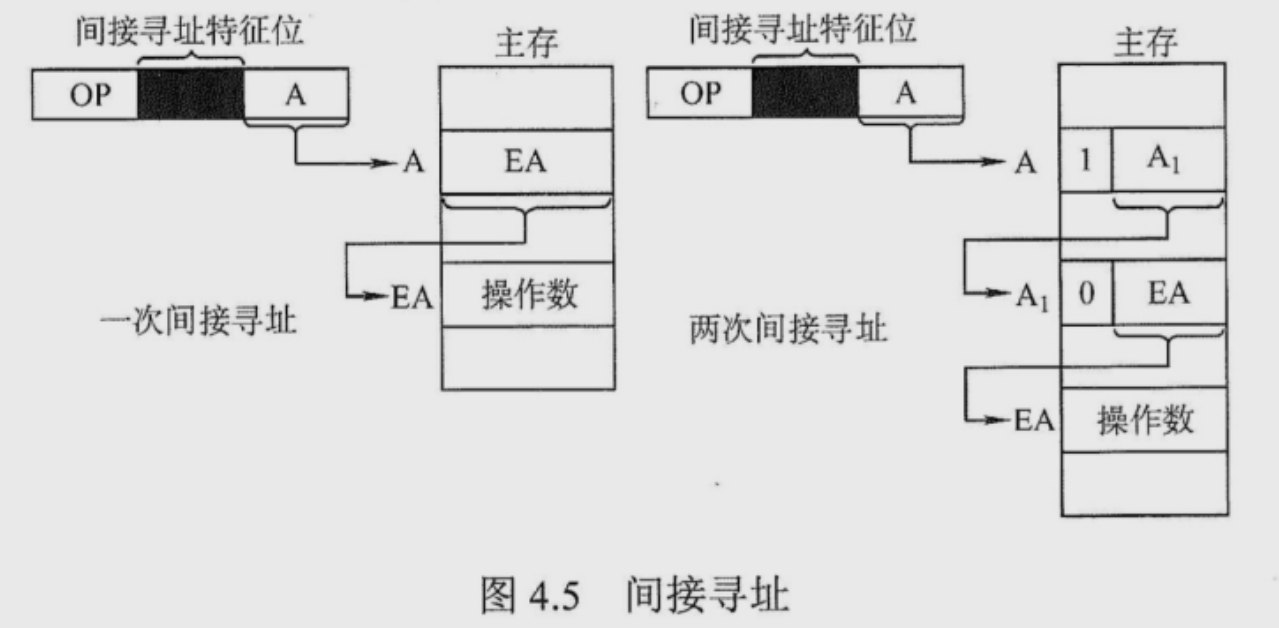
主存字第一位为1时，表示取出的仍不是操作数的地址，即多次间址;主存字第一位为0时，表示取得的是操作数的地址。
寄存器寻址 EA=R
i指令字中给出操作数所在的寄存器编号R
i,操作数存在寄存器Ri内。不用访存，速度快，但是价格昂贵，寄存器数量有限
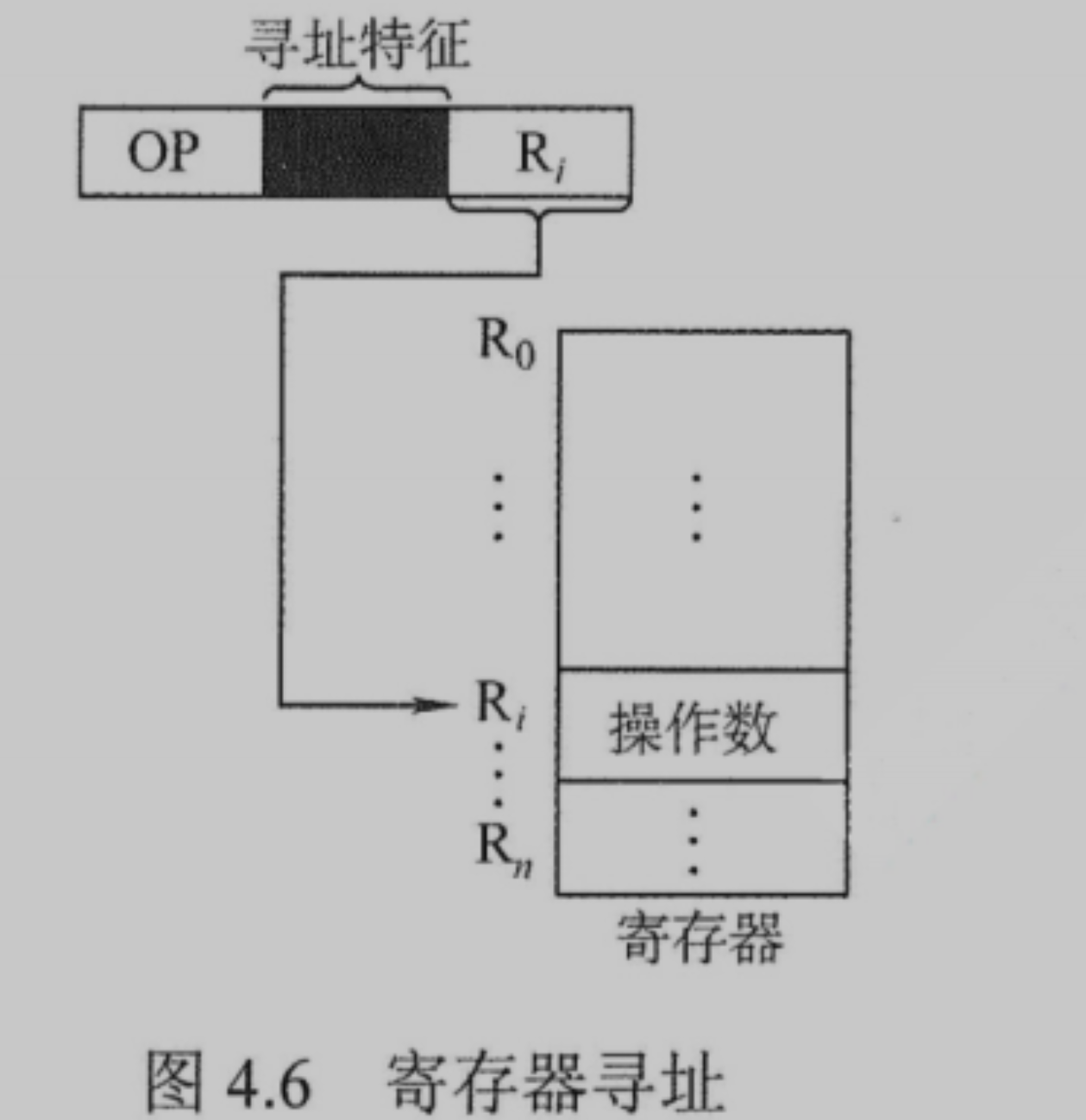
寄存器间接寻址 EA = (Ri)
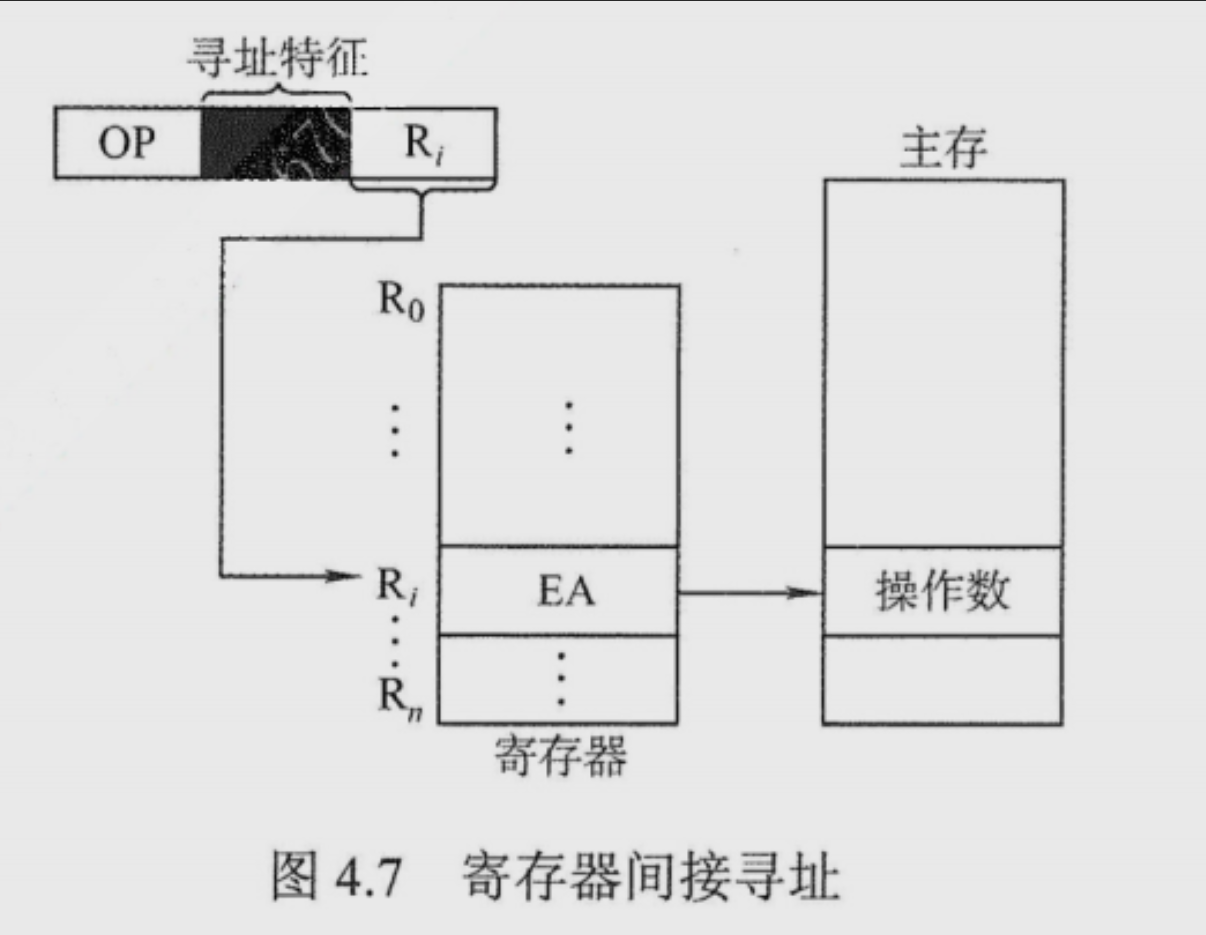需要访问主存相对寻址 EA = (PC)+A
A是相对于当前指令地址的地址，相对寻址的优点是操作数的地址不是固定的，它随PC值的变化而变化，且与指令地址之间总是相差一个固定值，因此便于程序浮动。相对寻址广泛应用于转移指令，比如JMP。
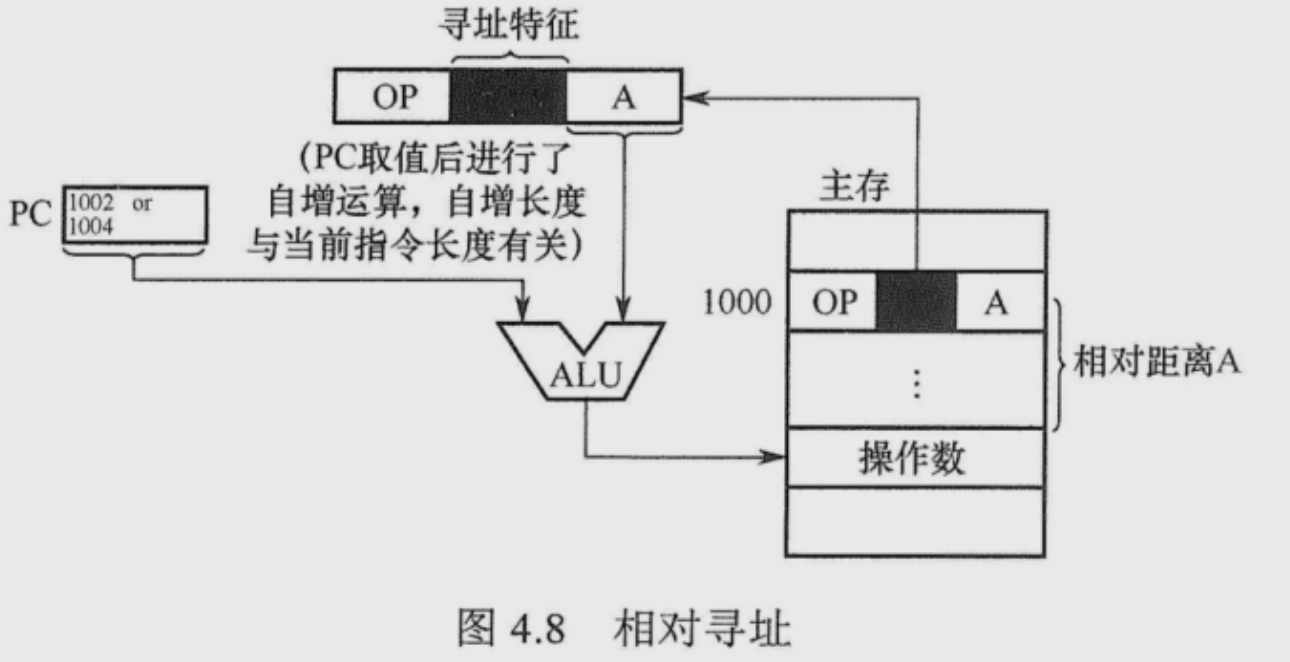
执行一条指令就是读取(PC)然后PC+”1”，那么运用相对寻址的时候，取完这条指令就已经+”1”了，相对位移量是A，所以转移到的地址是(PC)+”1”+A
基址寻址 EA =(BR)+ A
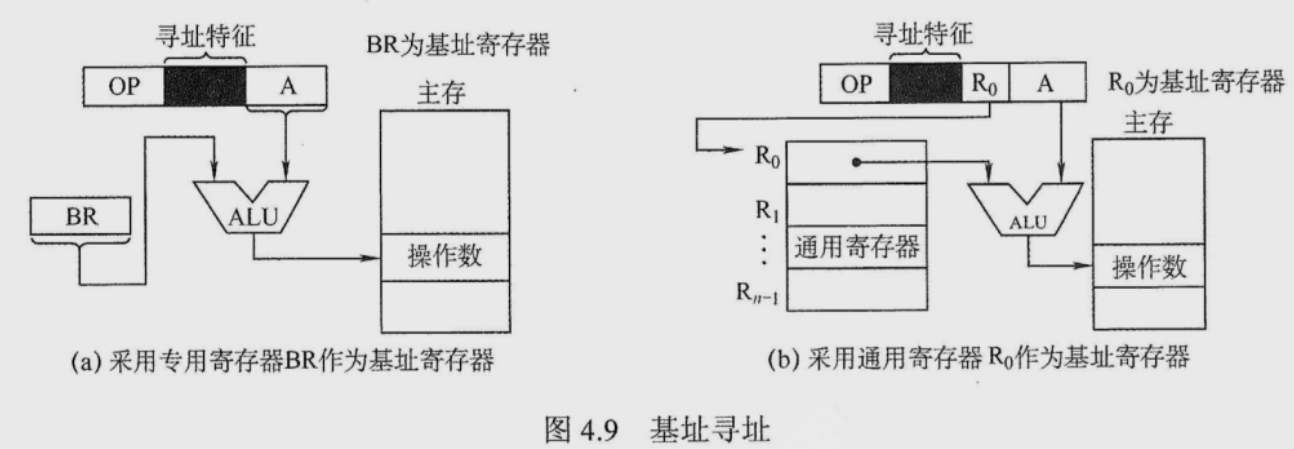
面向操作系统，由操作系统确定(BR), 一般是不可变的,A可变
变址寻址 EA = (IX)+A
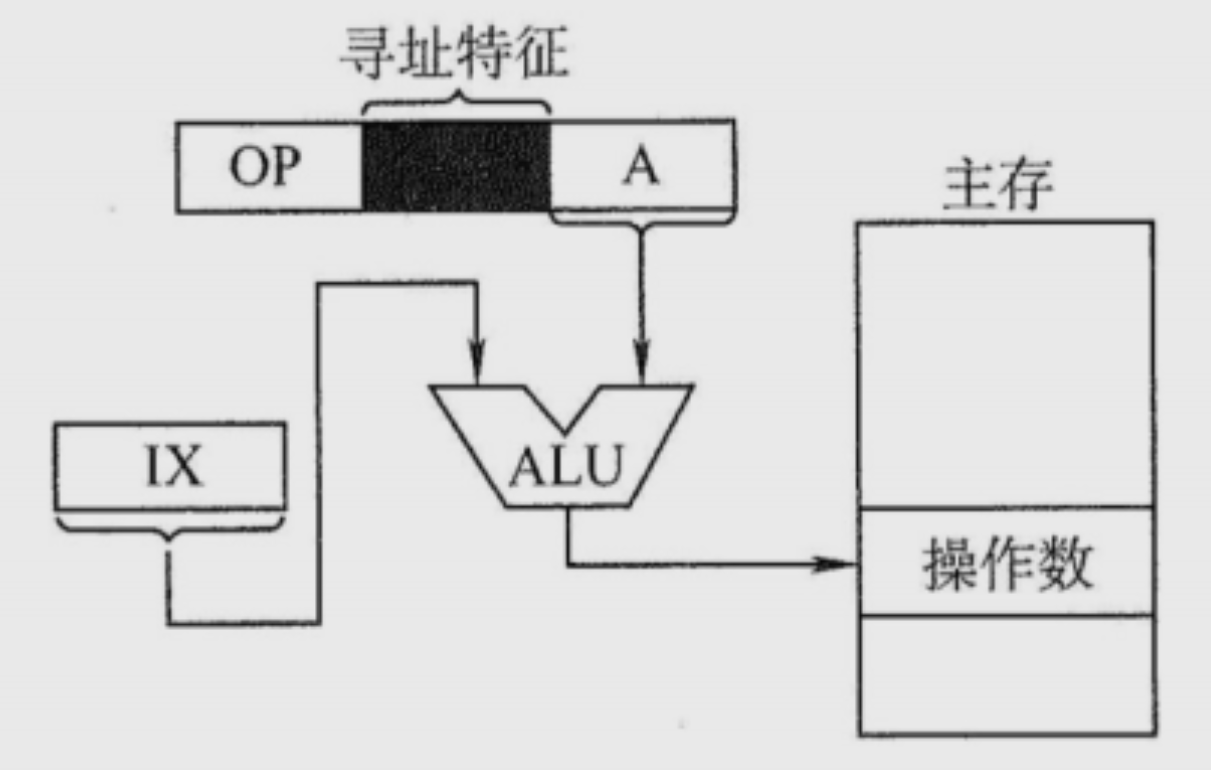
面向用户，(IX)可变，A不可变
不需要访存的：
- 立即寻址 （A就是操作数）
- 隐含寻址（操作数可以隐含保存在特定寄存器中）
- 寄存器寻址（操作数保存在寄存器中）
需要访存2次：
- 一次间接寻址（EA=(A) A先访存1次，然后根据(A)再访存1次）
以上不包含为了取本条指令而做的访存
- 堆栈寻址
堆栈是存储器（或专用寄存器组）中一块特定的、按后进先出（LIFO）原则管理的存储区，该存储区中读/写单元的地址是用一个特定的寄存器给出的，该寄存器称为堆栈指针(SP)。 堆栈堆栈 可分为 硬堆栈硬堆栈 与 软堆栈软堆栈 两种。
寄存器堆栈又称硬堆栈。寄存器堆栈的成本较高，不适合做大容量的堆栈;而从主存中划出一段区域来做堆栈是最合算且最常用的方法，这种堆栈称为软堆栈。
在采用堆栈结构的计算机系统中，大部分指令表面上都表现为无操作数指令的形式，因为操作数地址都隐含使用了SP。通常情况下，在读/写堆栈中的一个单元的前后都伴有自动完成对SP内容的增量或减量操作。
Example
1）寄存器-存储器（R-S）指令格式：操作码OPcode+寄存器位R+特征位+形式地址A
32个寄存器，编号需要5位，64种操作->操作码6位000000-111111，特征位由于只有直接或间接寻址，所以只要1位特征位即可，剩下即为形式地址。
OP(6)+R(5)+特征位(1)+A(20)
20位形式地址，最多直接寻址的空间为1M存储字，
如果是间接寻址就可以扩大寻址空间，最多到2^32^=4G字
2）通用寄存器，寻址方式多了一种基址方式，基址寄存器中的内容是特定不变的，OP(6)+R(5)+特征位(2)+A(19)？但是应该指明用哪一个通用寄存器作为基址寄存器
OP(6)+R(5)+特征位(2)+BR(5)+A(14)
通用寄存器有32位，所以使用基址寻址的最大寻址空间=2^32^=4G字，仅仅与基址位数有关
指令格式
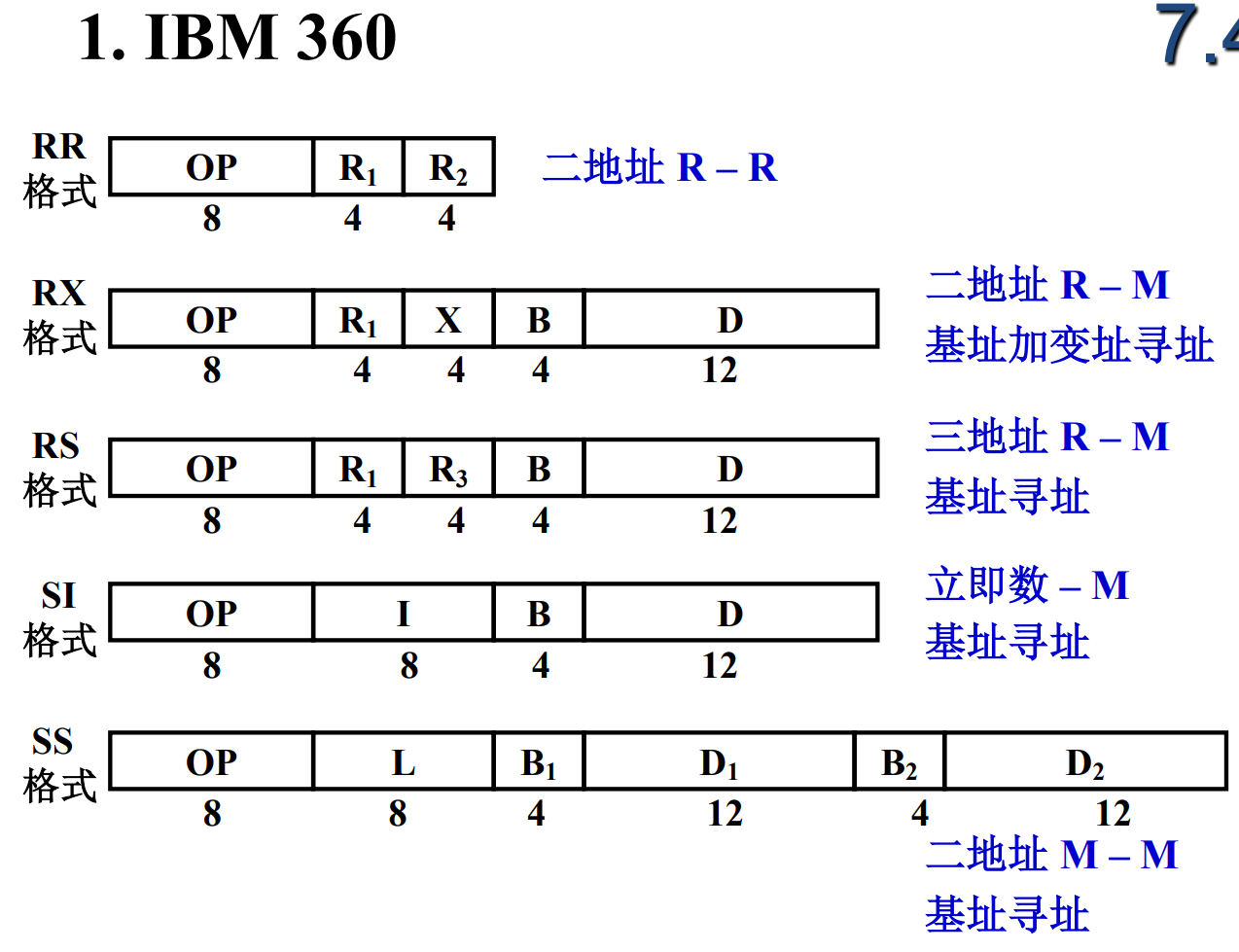
RISC
Reduced Instruction Set Computer 精简指令集计算机
与C(omplex)ISC相对
二八定律
RISC:
- 指令长度固定，指令格式种类少，寻址方式少；
- 只使用LOAD STORE访存，通用寄存器较多；
- 流水线技术，一个时钟周期内完成一条指令；
- 控制器运用组合逻辑。
CISC:
- 指令庞杂，指令使用频度相差较大，长度不固定，种类多
- 很多指令可以访存
- CPU有专用寄存器
- 大部分指令都需要多个时钟周期完成
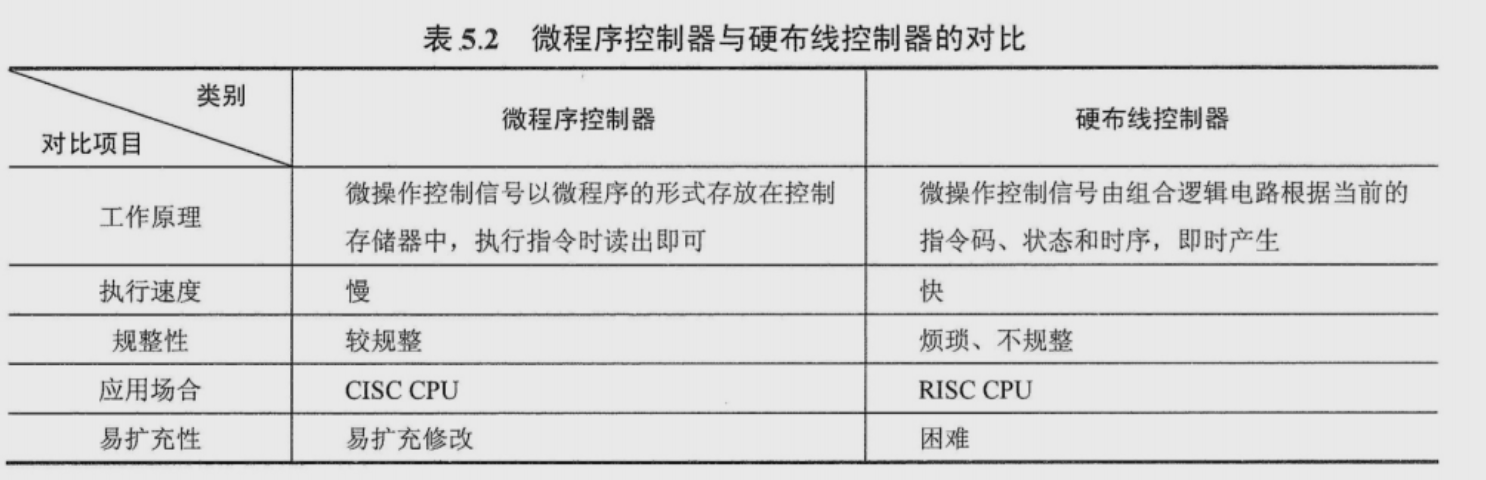
- 采用微程序控制器
值得注意的是，从指令系统兼容性看，CISC大多能实现软件兼容，即高档机包含了低档机的全部指令，并可加以扩充。但RISC简化了指令系统，指令条数少，格式也不同于老机器，因此大多数RISC机不能与老机器兼容。由于 RISC具有更强的实用性，因此应该是未来处理器的发展方向。但事实上，当今时代Intel 几乎一统江湖，且早期很多软件都是根据CISC 设计的，单纯的RISC将无法兼容。此外，现代CISC结构的CPU已经融合了很多RISC的成分，其性能差距已经越来越小。CISC可以提供更多的功能，这是程序设计所需要的。
RISC利用VLSI芯片的面积，便于设计，降低成本，提高可靠性，但是不容易实现指令系统的兼容
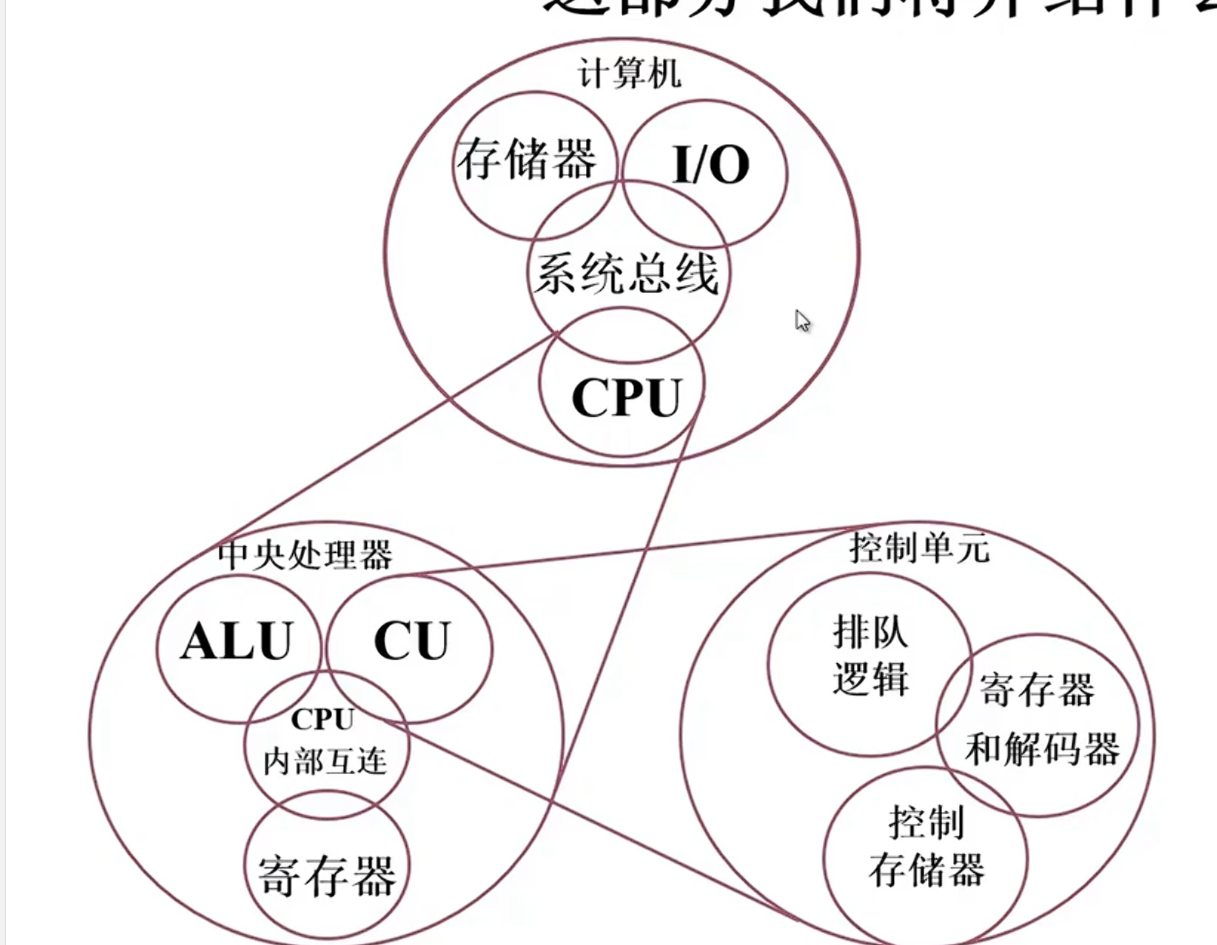
CPU
CPU的结构
指令控制 PC IR
操作控制、时间控制 CU 时序电路
数据加工 ALU (运算器) + 寄存器
中断处理 中断系统
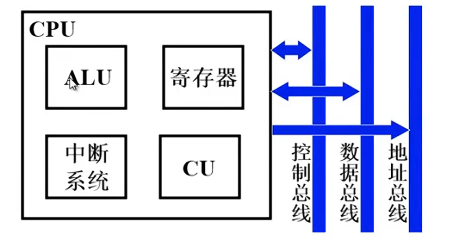
CPU的寄存器
用户可见寄存器
通用寄存器 General Register
- 存放操作数
- 作为某种寻址方式所需要的专用寄存器
数据寄存器 Data Register
- 存放多种操作数（多种数据类型）
- 两个寄存器拼接存放双倍字长的数据[ACC和MQ]
地址寄存器
- 存放地址，位数满足最大的地址的范围，用于特殊的寻址方式，段基值，栈指针
条件码寄存器
- 存放条件码，作为程序分支的依据，入如正负零，溢出，进位
控制和状态寄存器
控制寄存器
状态寄存器
- 存放条件码
- PSW 存放程序状态字，中断服务程序或者子程序，为了保存运行现场和断点。
控制单元CU和中断系统
- 产生全部指令的微操作命令序列
- 组合逻辑(RISC) 硬连线逻辑
- 微程序设计 存储逻辑
ALU
指令周期
- 指令周期=取址周期
- 指令周期=取址周期+执行周期(等长)
- 指令周期=取址周期+执行周期(长一些)
- 间接寻址的指令周期=取址周期+间址周期+执行周期
- 中断周期的指令周期=取址周期+间址周期+执行周期+中断周期
流程：
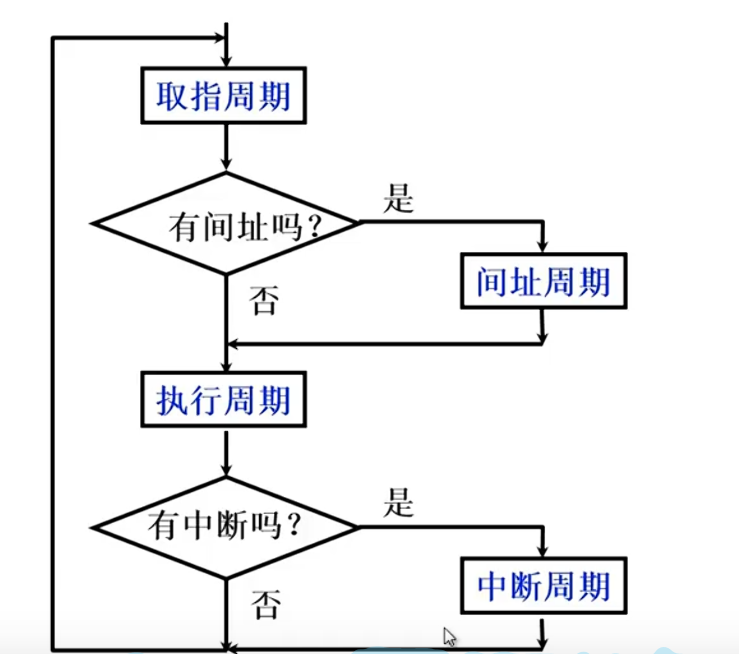
CPU访存有4种性质
- 取 指令 取指周期
- 取 地址 间址周期
- 存取 操作数 执行周期
- 存 程序断点 中断周期
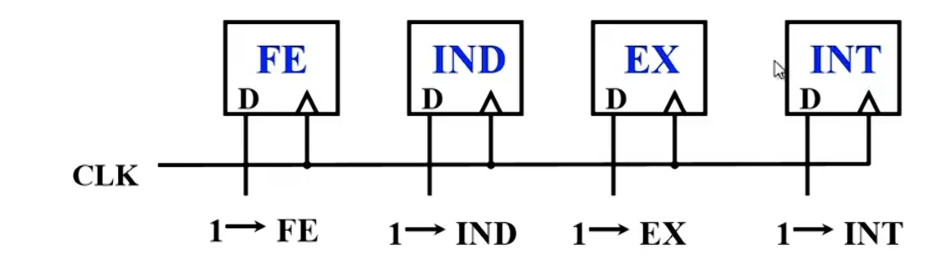
数据流
取指周期
PC寄存器存的是下一条指令的地址，CU通过控制总线，控制地址通过MAR传到地址总线，（读命令）地址总线传到存储器，控制存储器将对应的数据（指令）通过数据总线传到MDR，最后保存到CPU的IR寄存器中。CU控制PC寄存器的值+“1”
间址周期
假设取完指令以后将形式地址A保存到了MDR，此时A的值传给MAR，通过地址总线传给存储器，CU控制总线让存储器取出A中保存的数据(A)也就是EA，EA保存到MDR，操作数的真实地址EA最后保存到了IR的地址码部分
执行周期
中断周期
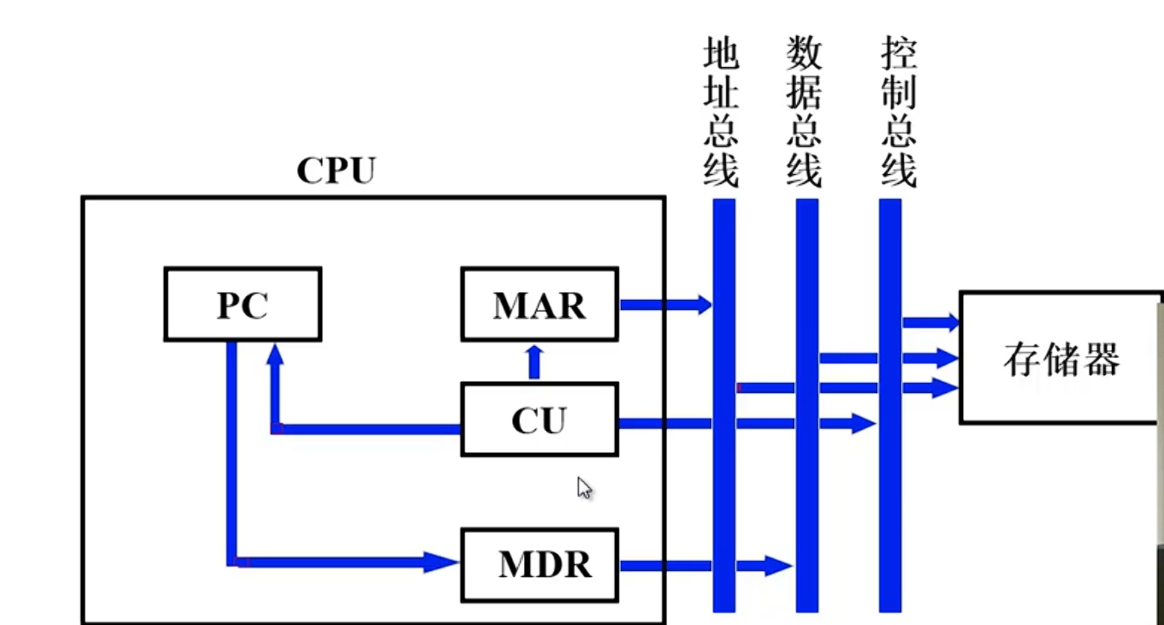
保存断点，形成中断服务程序的入口地址（中断向量），硬件关中断
保存程序断点，CU来确定将程序断点保存到内存的哪个地址，传给MAR，存储器，CU再控制总线操控存储器进行写入断点的操作，由于响应中断一定是在执行完一条指令之后，所以下一条指令还没有取到，下一条指令的地址就是(PC)，将PC存储的值送到MDR，再通过数据总线写入存储器。
形成中断服务程序的入口地址：CU给出送到PC
(关中断)
指令流水
提高机器速度？
提高访存速度：Cache 多体并行
提高IO和主机的传送速度：
- 中断，部分时间并行
- DMA，几乎全部并行
- 通道，I/O处理机
- 多总线
提高运算速度：
- 高速芯片，改进算法，快速进位链
提高并行性
系统并行
并行：并发 / 同时。多个事件在同一时间段或同一时刻，并行发生
并行性的等级：
指令流水原理
CU中取指和执行部件完全独立的两个部件。
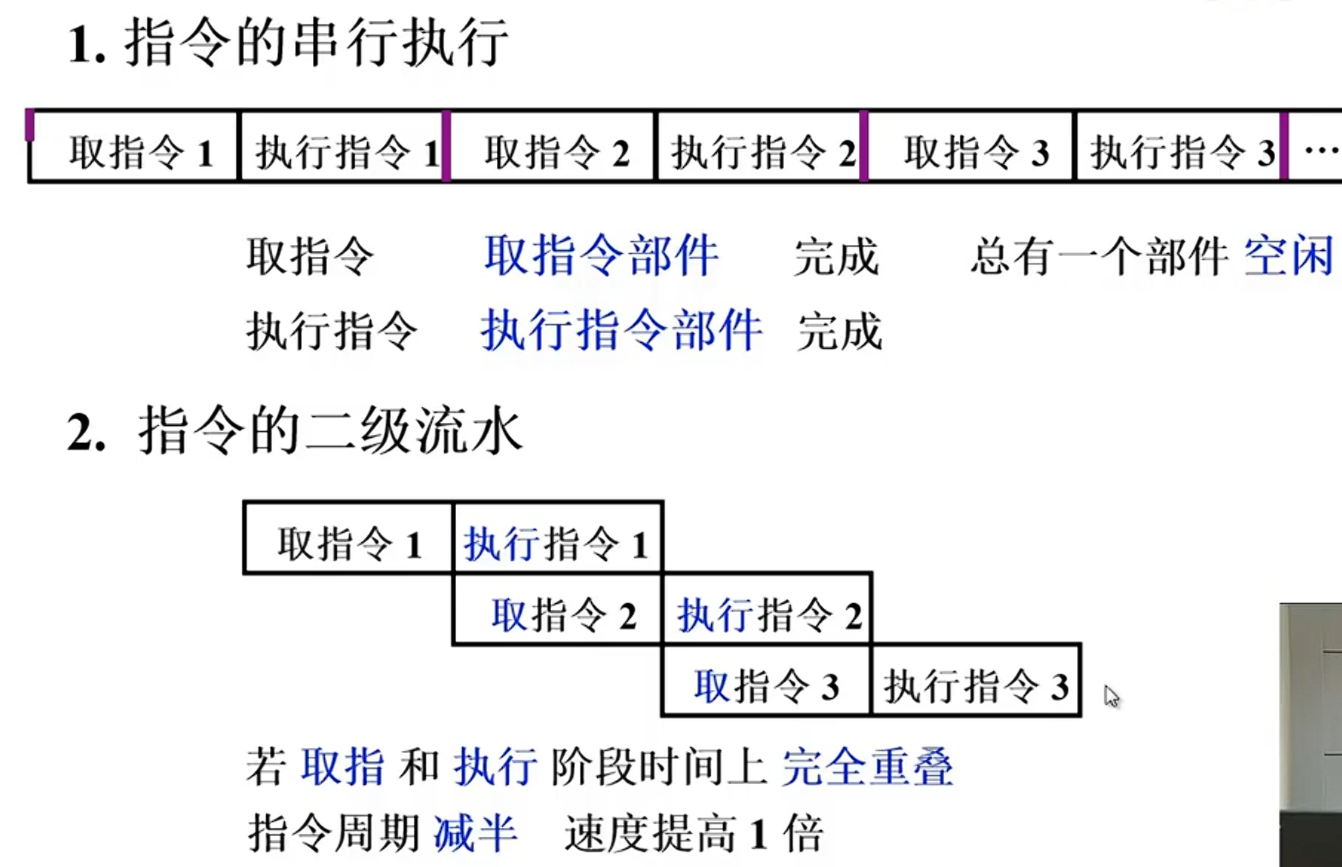
二级流水，执行的时候同时取第二条指令
影响因素：
取指时间快的话，指令2的执行就要空等。
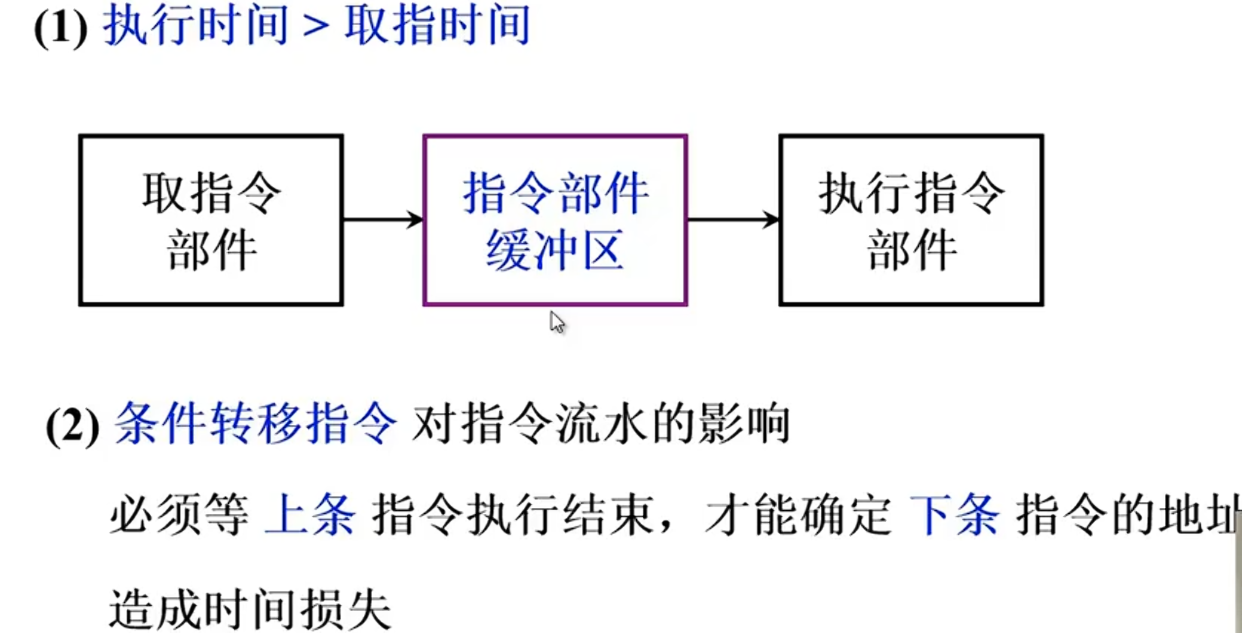
“分支预测” 猜测？
六级流水
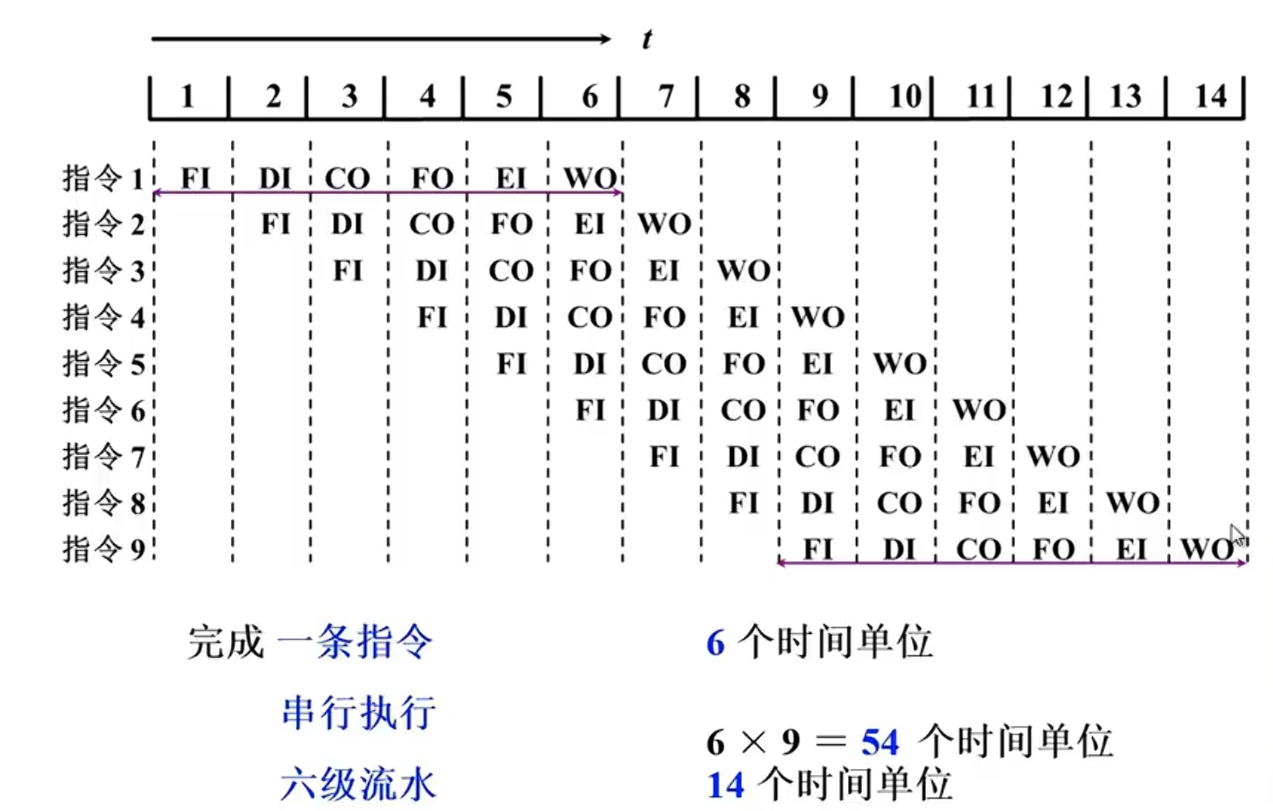
影响性能因素
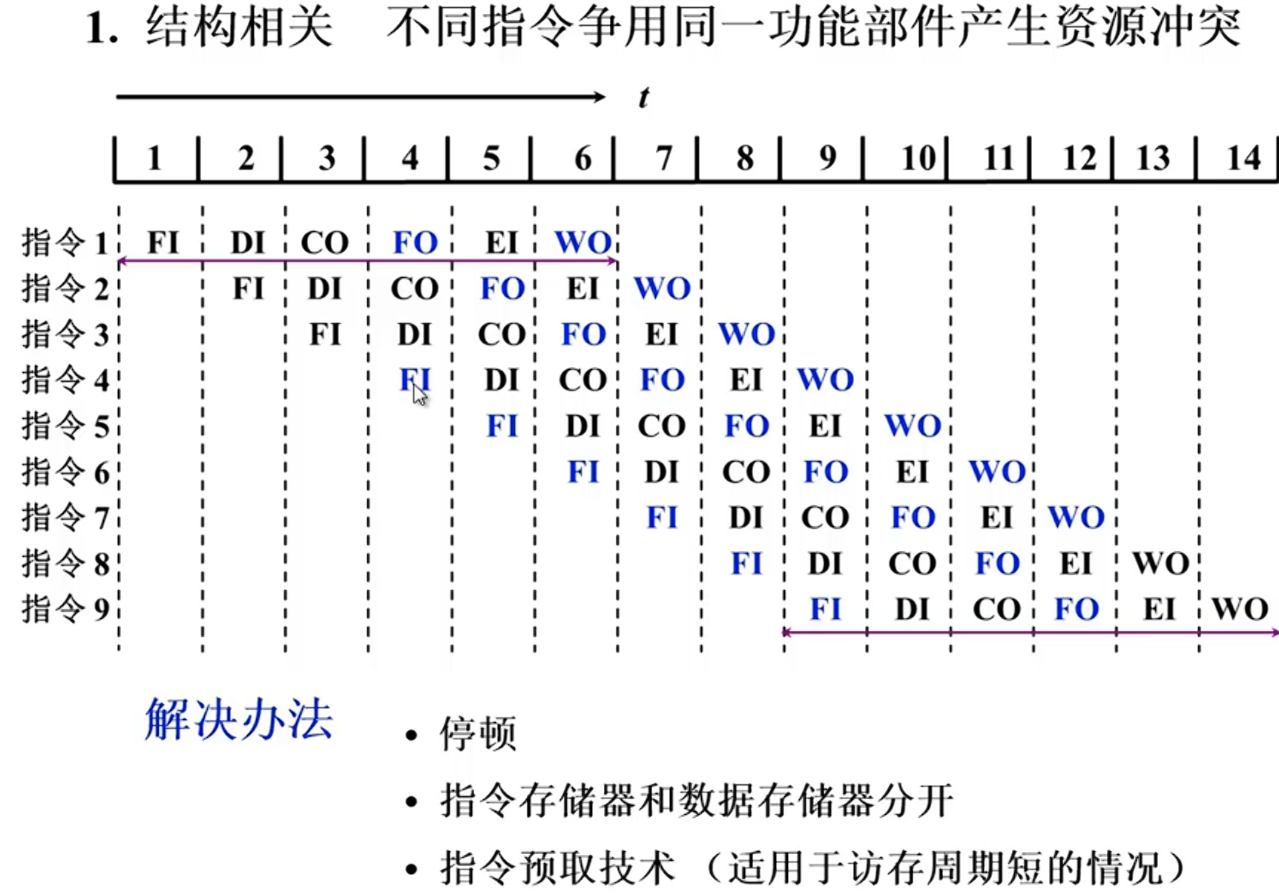
WAW R3不知道是谁写入的
解决办法 后推、旁路技术
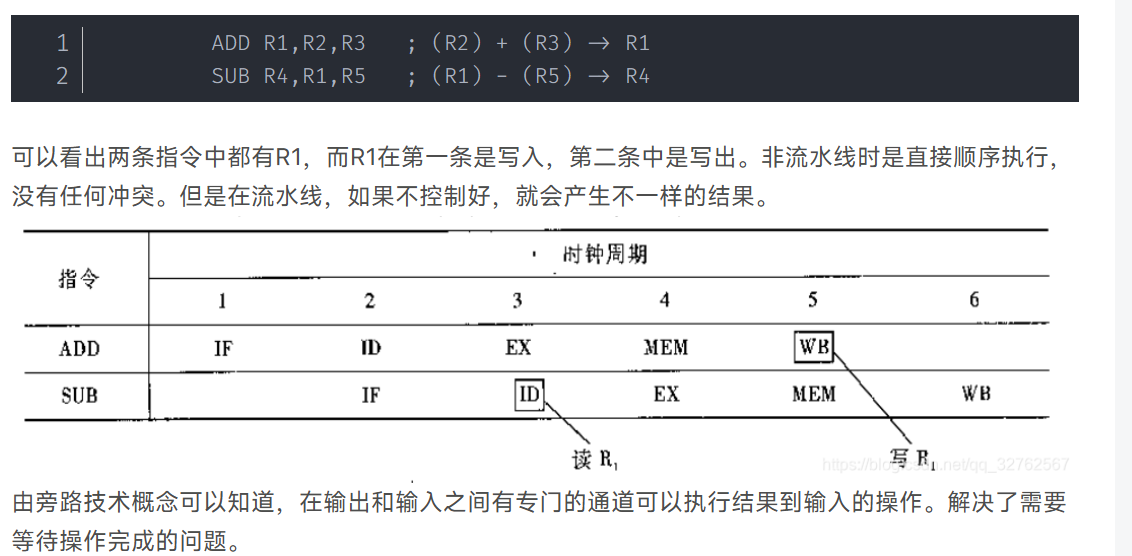
EX阶段就已经给出了结果值，不必待某条指令的执行结果送回到寄存器后，再从寄存器中取出结果。作为下一条指令的源操 作数，而是直接将执行结果送到其他指令所需要的地方
转移指令直到EI结束才知道是否要转移
流水线多发
一条流水线实现了时间并行性
多条流水线还能体现空间并行性
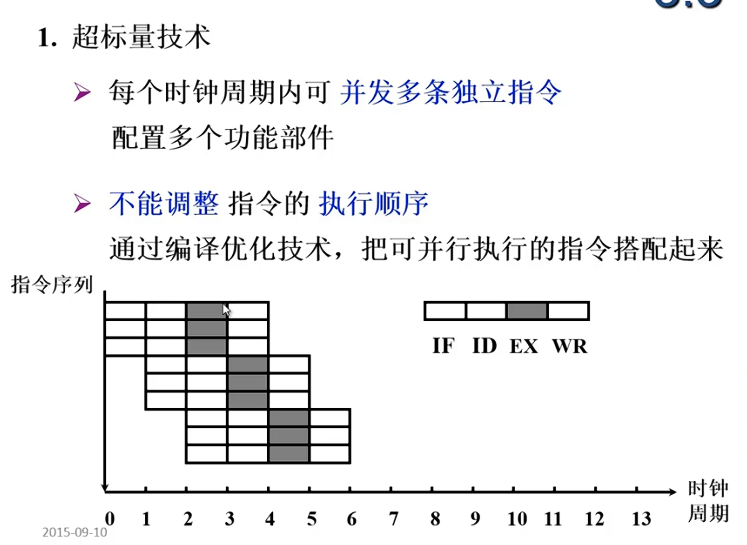
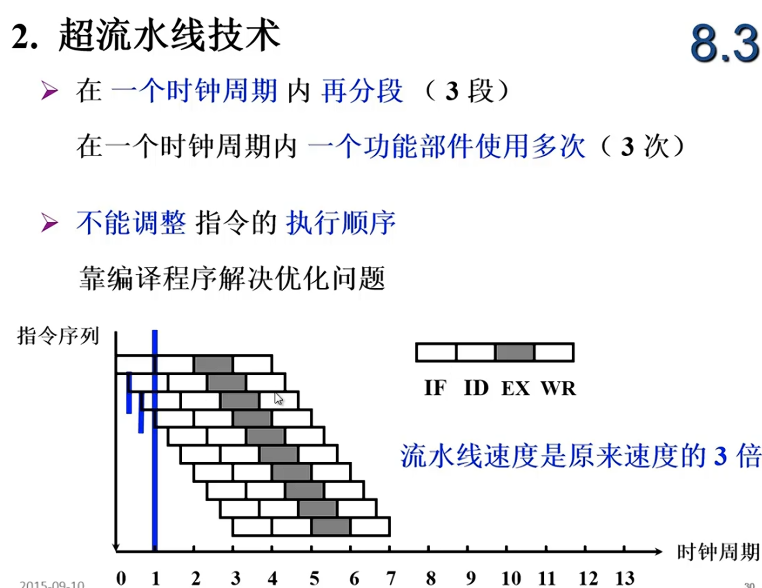
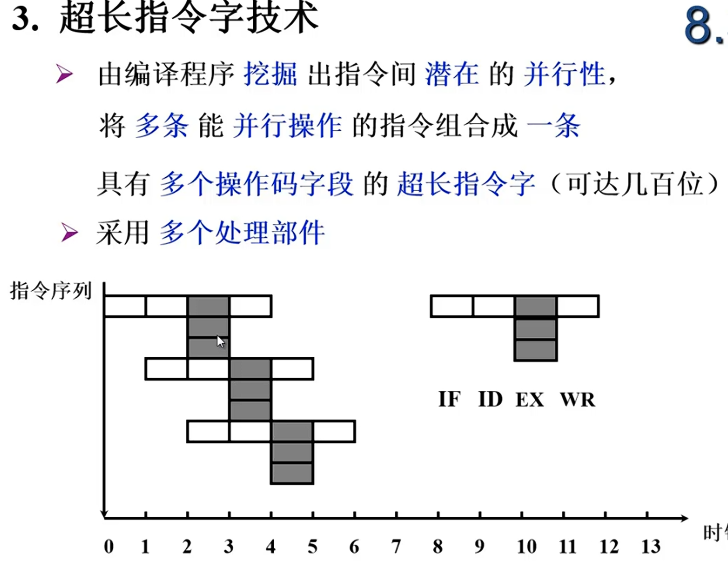
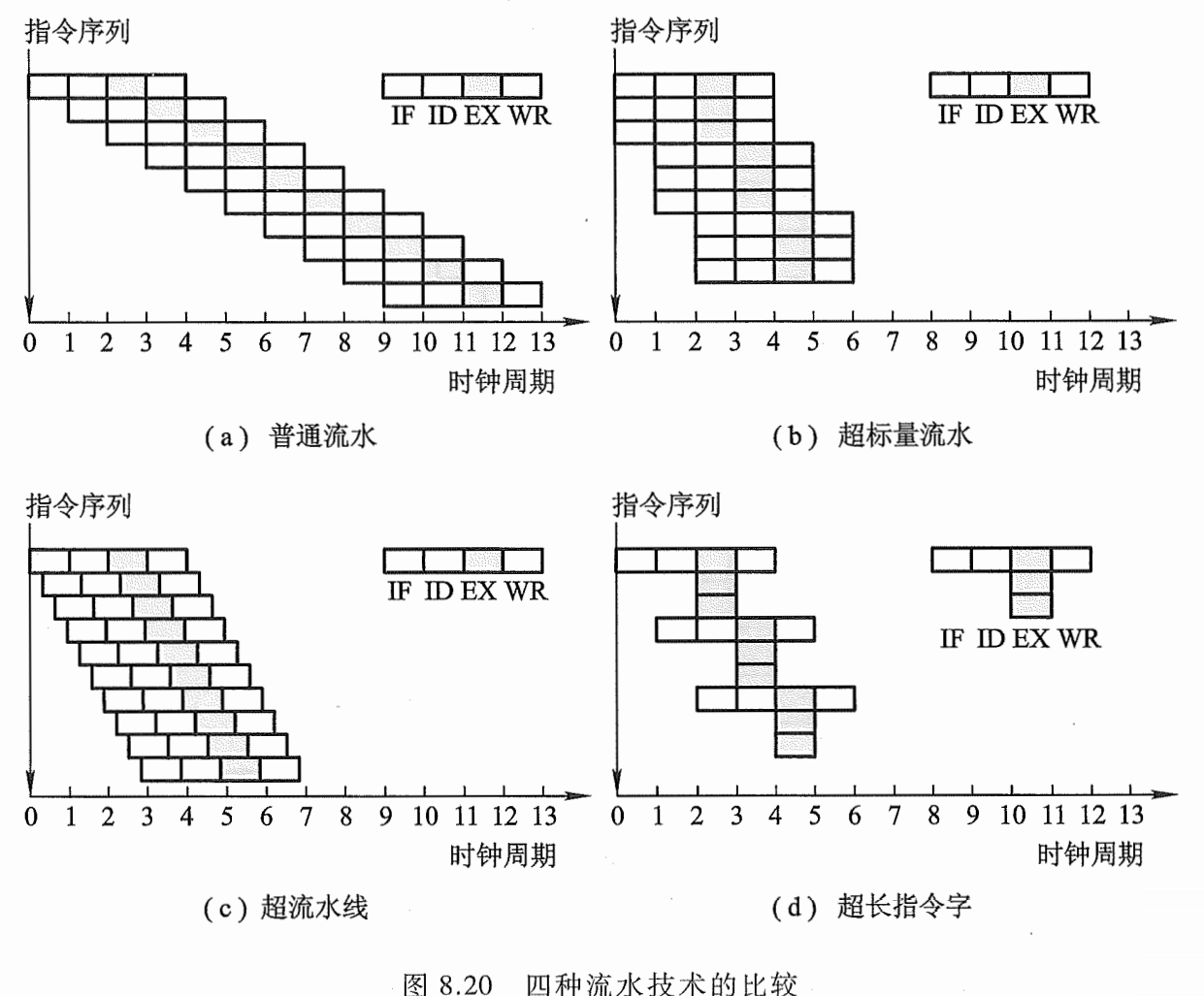
流水线结构
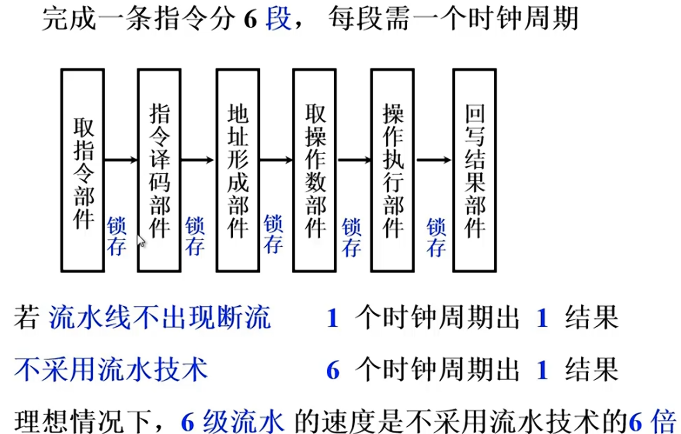
运算过程比较复杂的可以使用运算流水线
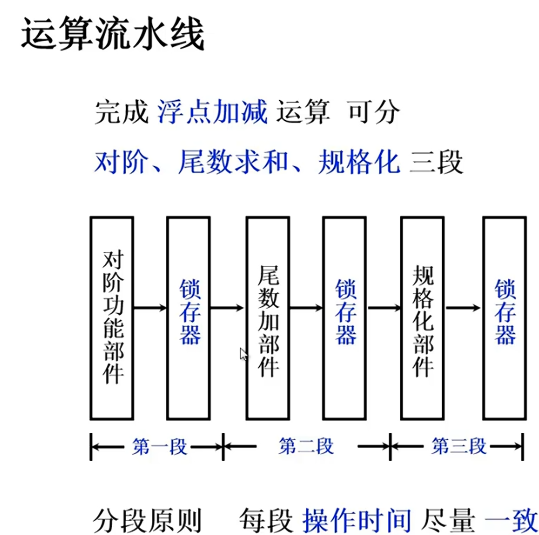
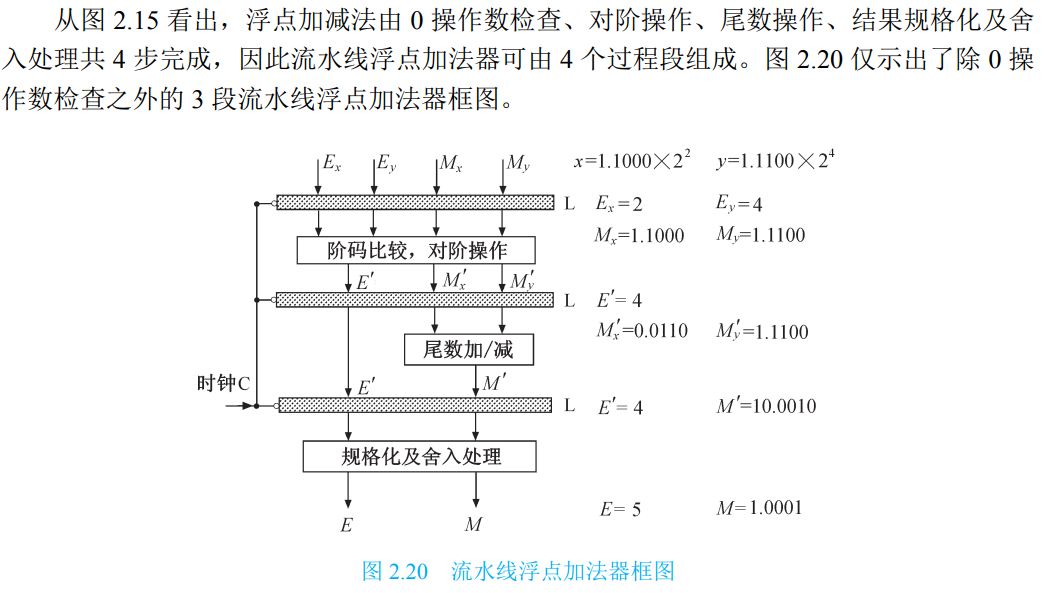
一个任务分割为多个子任务，原则上要求时间上等分，子任务由不同的部件完成，如果不等分，指令1执行过程中取到了指令2，但是指令2必须等到1执行完才开始执行，这就造成了任务的空窗期，造成了时间的浪费
中断系统
引起中断的因素
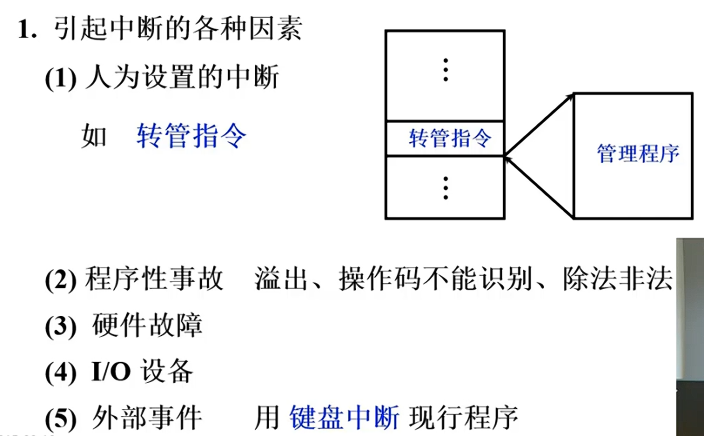
中断系统解决的问题
中断请求处理
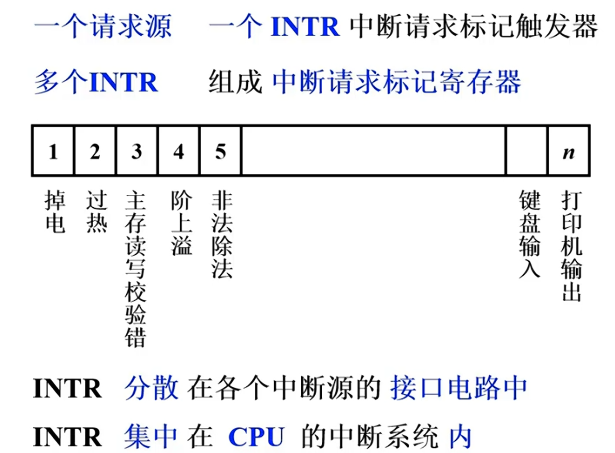
中断判优逻辑
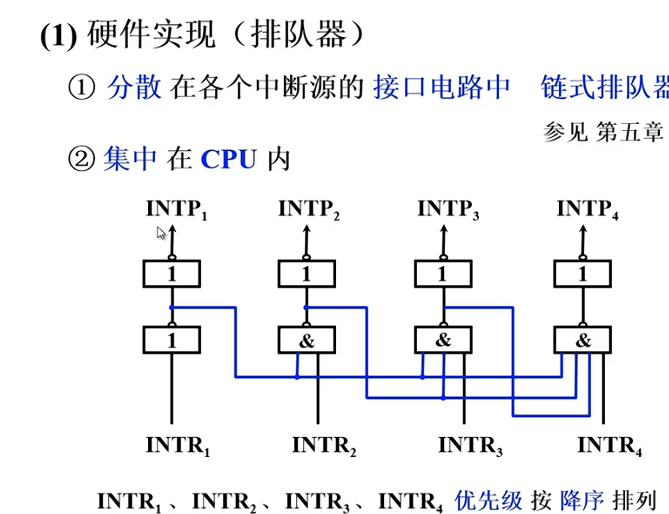
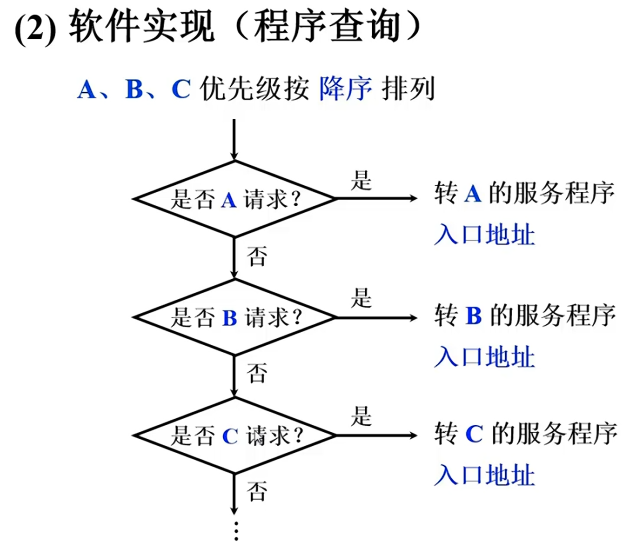
中断服务程序入口地址
硬件向量法，速度快，但不灵活
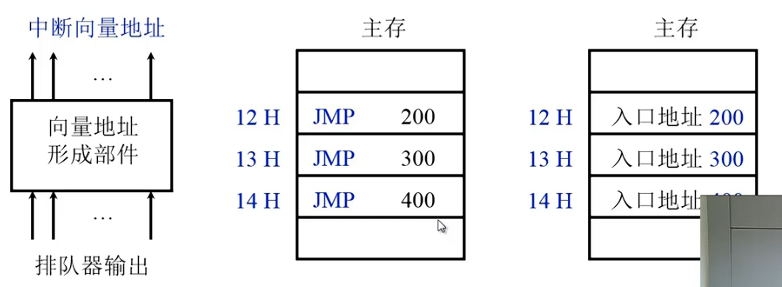
软件查询法，使用中断识别程序
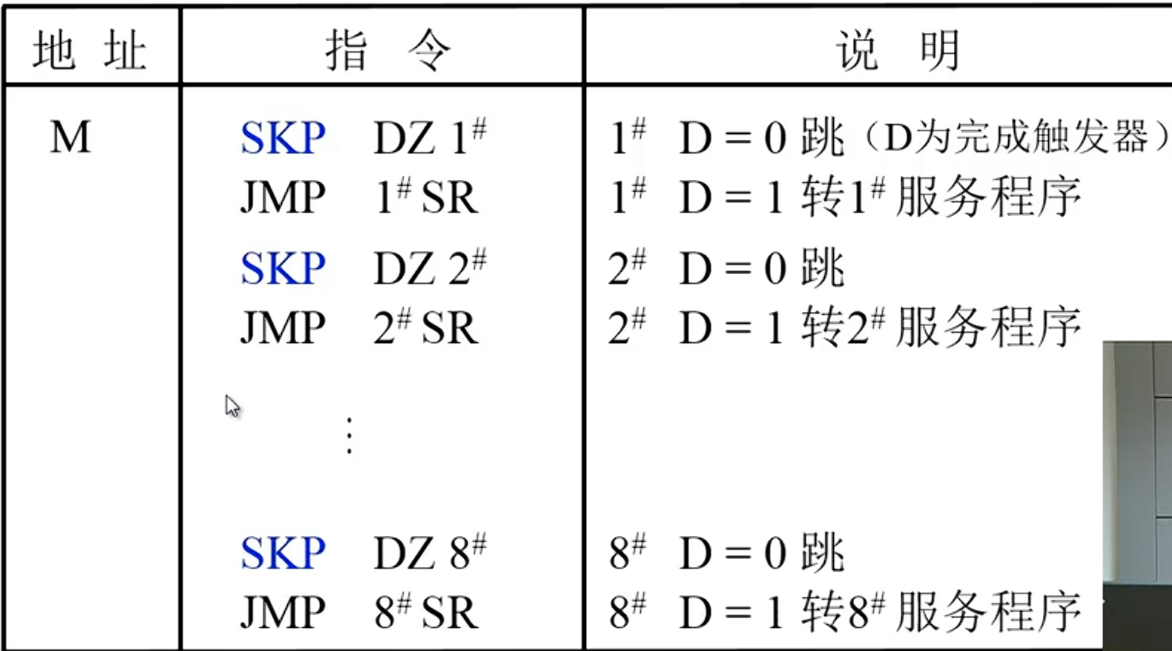
中断响应
响应条件
- 允许中断触发器 EINT=1
- 一条指令执行结束时由CPU发查询信号
中断隐指令(硬件实现，并不在指令集中)
保护程序断点
- 断点保存到特定地址
- 断点进栈
寻找服务程序入口地址
- 硬件向量
- 中断识别程序M->PC 软件
关中断 EINT = 0
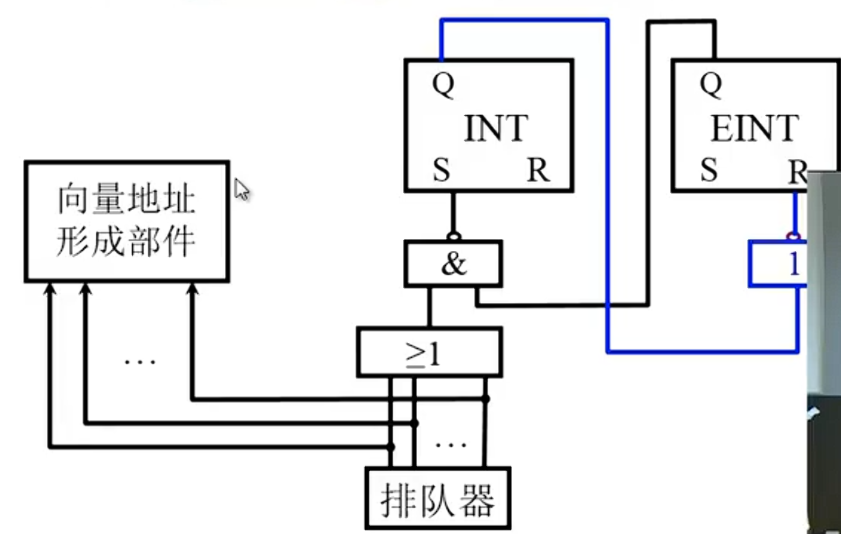
保护、恢复现场
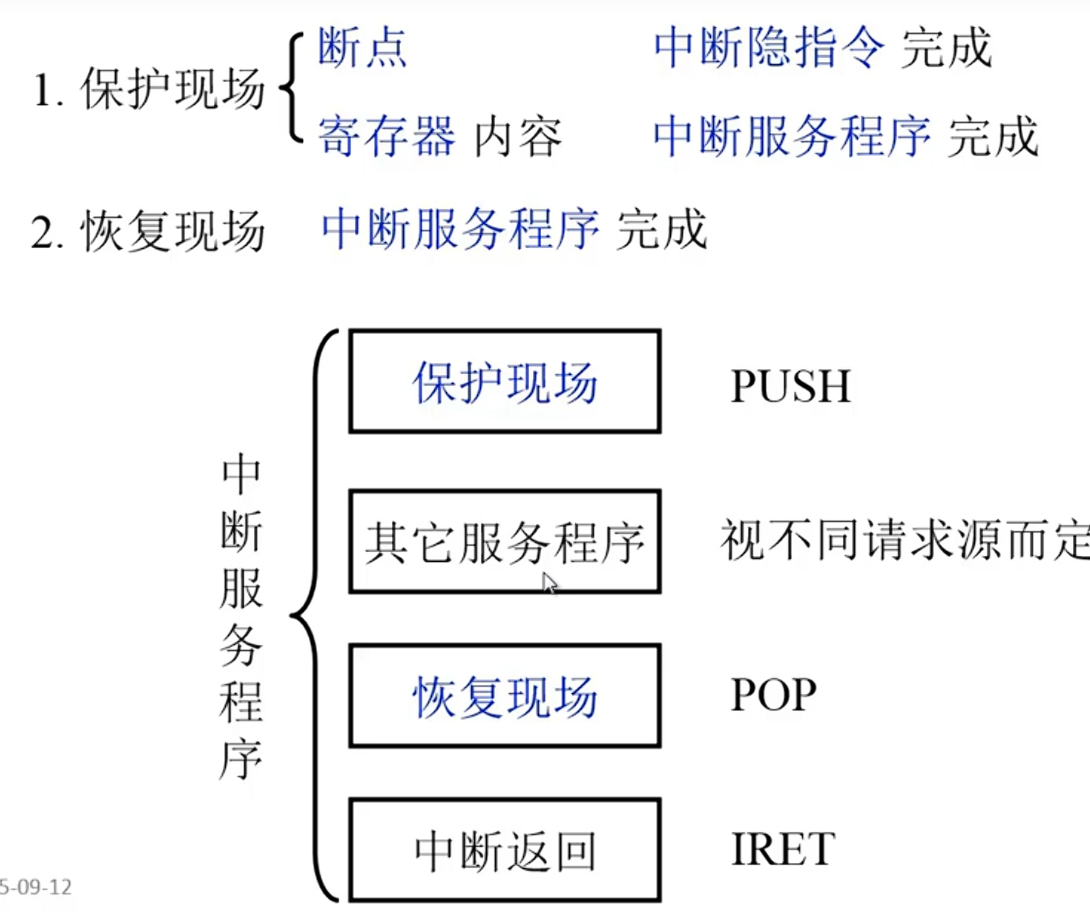
多重中断
提前设置 开中断 指令
优先级高可以打断优先级低的处理程序
中断屏蔽技术
MASK 触发器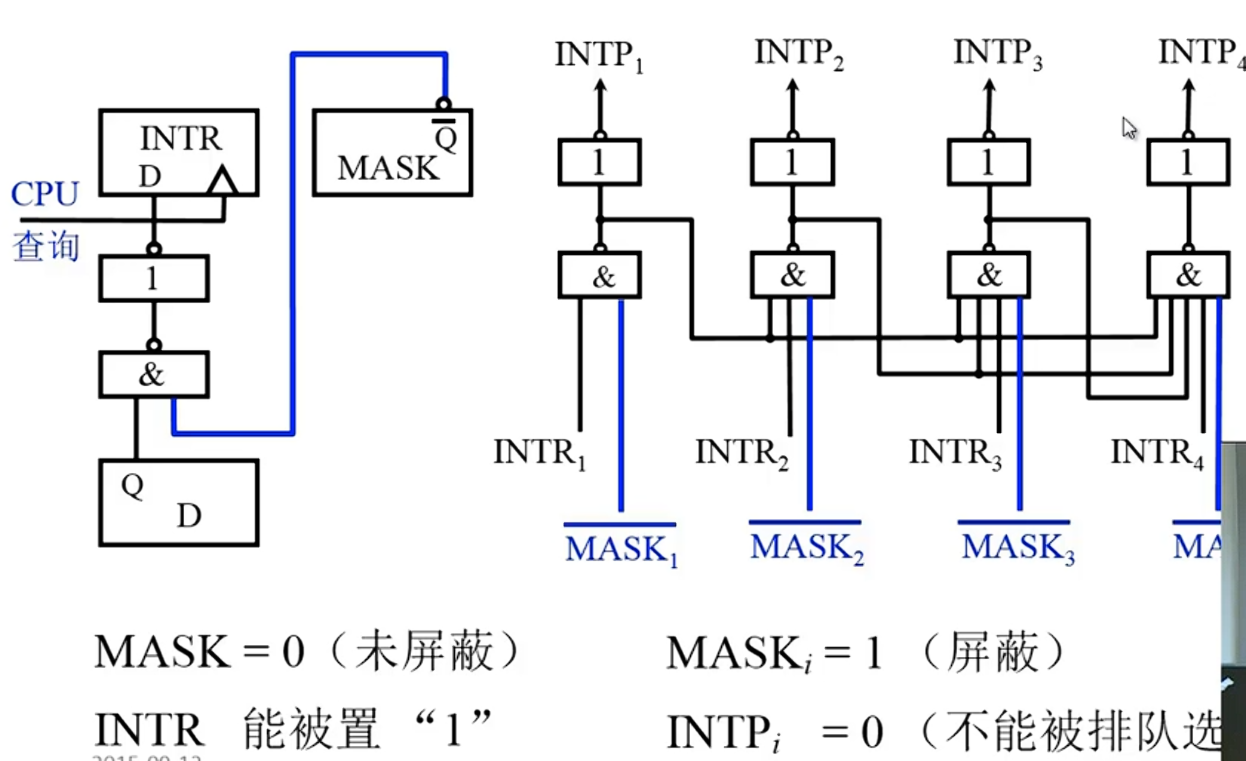 
屏蔽字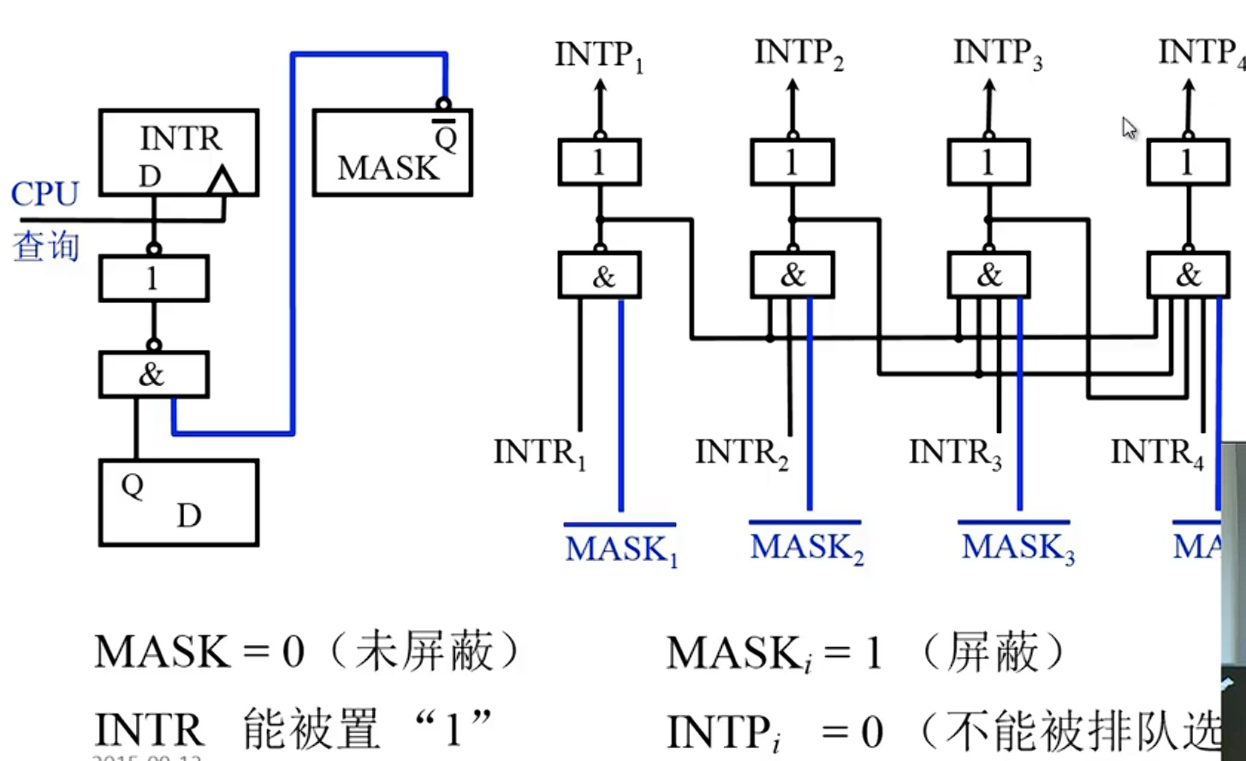
响应优先级不可以改变，处理优先级可以改变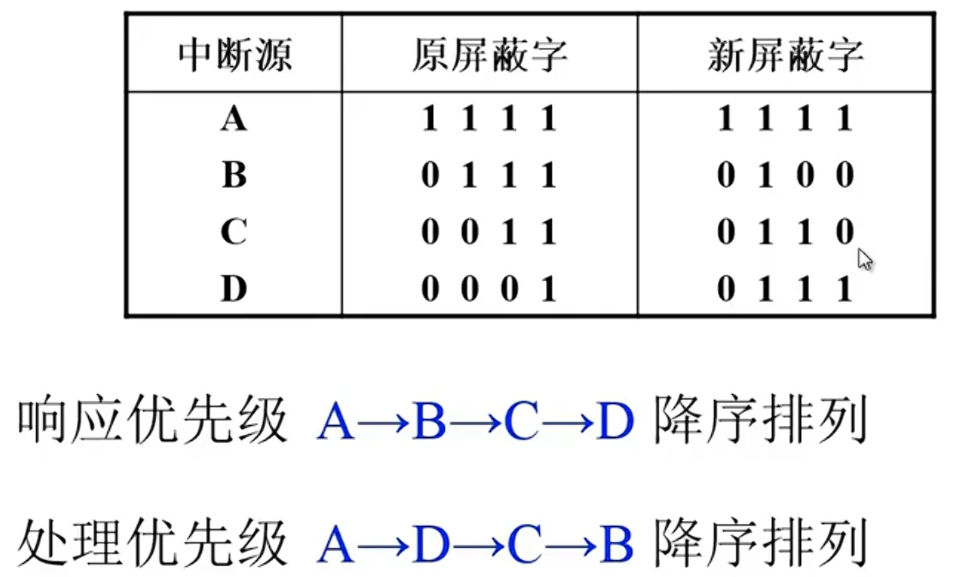
中断源响应之后会设置各个中断源的屏蔽字MASK[]
应用：可以人为屏蔽某个中断源
设置新屏蔽字：保护现场之后，置屏蔽字，然后开中断（为了实现多重中断），进行中断服务，恢复现场和恢复屏蔽字之前要关中断，确保正确恢复，最后开中断，中断返回
断点保护
断点进栈
断点存入“0”地址
CU将“0”地址写入MAR，准备写操作，PC的值写入MDR然后再进入存储器
出现了断点覆盖的问题
保护断点的做法，不同的服务程序将断点保存到不同的地址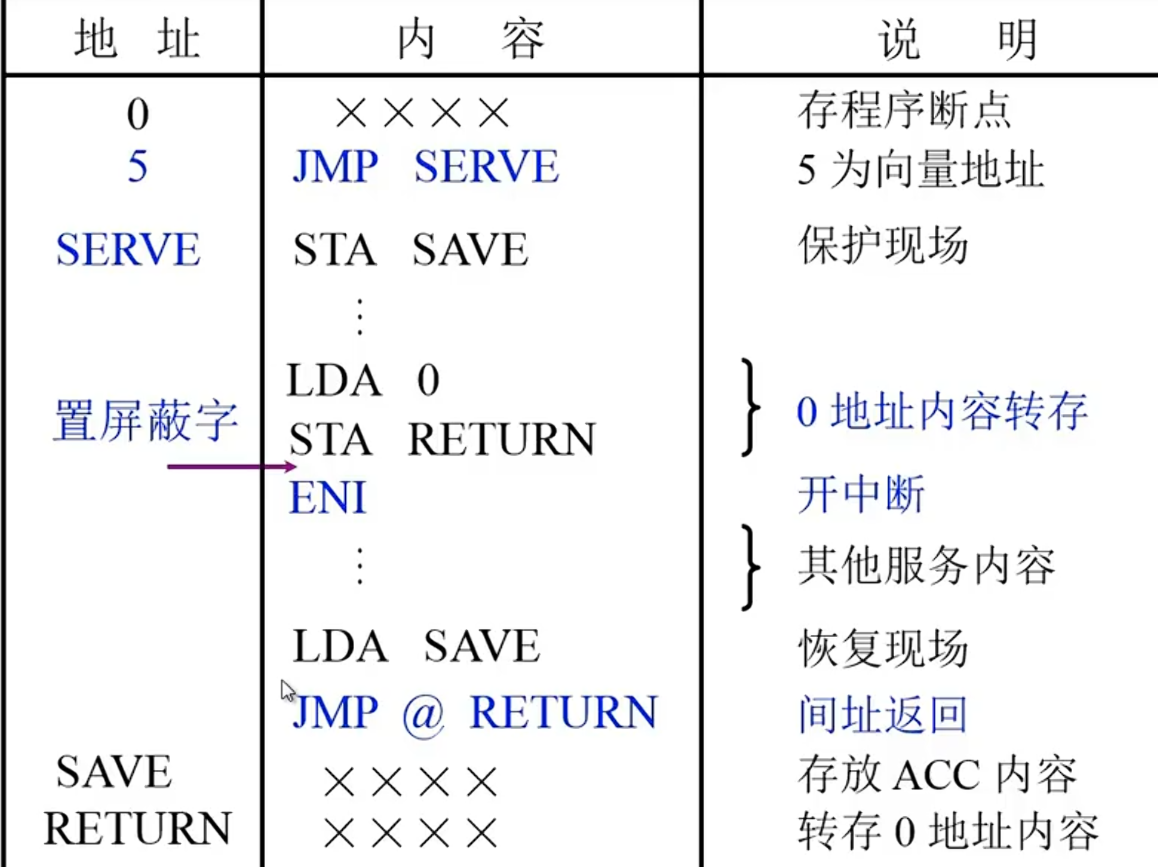
STA(Store Accmulator) SAVE 将ACC原来的值保存到SAVE中
LDA(Load Accumulator) 0将0地址的内容(程序断点)保存到ACC
STA RETURN 将0地址保存到RETURN中
JMP @ RETURN 无条件跳转到RETURN保存的地址
每个SERVE程序 都有不同的RETURN 把0地址的内容转存到各自的RETURN即可
控制单元 CU
微操作命令分析
解释指令的过程中，CU发出的操作就叫微操作，比如加法指令，还能继续往下细分。
完成一条指令：取指，间址，执行，中断4个周期
取指周期
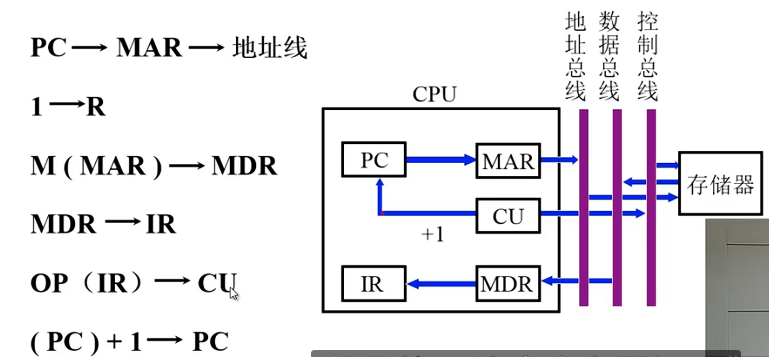
间址周期
执行周期
非访存指令(取指+执行)
访存指令(取指+执行)/(取指+间址+执行)
转移指令(取指+执行)
间接转移(取指+间址+执行)
中断周期
0地址：
- 0地址保存到MAR
- 1->W 写
- PC -> MDR
- MDR->M(MAR)
- 向量地址->PC / 中断识别程序 M->PC
- 0->EINT
断点进栈：
(SP)-1->MAR
1->W 写
PC -> MDR
MDR->M(MAR)
向量地址->PC / 中断识别程序 M->PC
0->EINT
控制单元
发出各种微指令
外特性
输入信号
- 时钟 受到clk控制
- 指令寄存器 控制信号和OPcode有关 用于译码
- 标志 受标志控制，上一条指令运行结果的标志，能够让CU决定这次运行是否跳转
- 外来信号 INTR 中断请求、HRQ总线请求
输出信号
- CPU内的控制信号
- Ri->Rj
- PC+1 -> PC
- ALU进行什么运算
- 送到控制总线的信号
- 访存控制信号$\overline{MREQ}$
- 访IO/存储器控制信号$\overline{IO}/M$
- 读写命令$\overline{RD}$ $\overline{WR}$
- 中断响应 INTA
- 总线响应 HLDA
控制信号
不采用总线
C0-C8均为门电路的控制
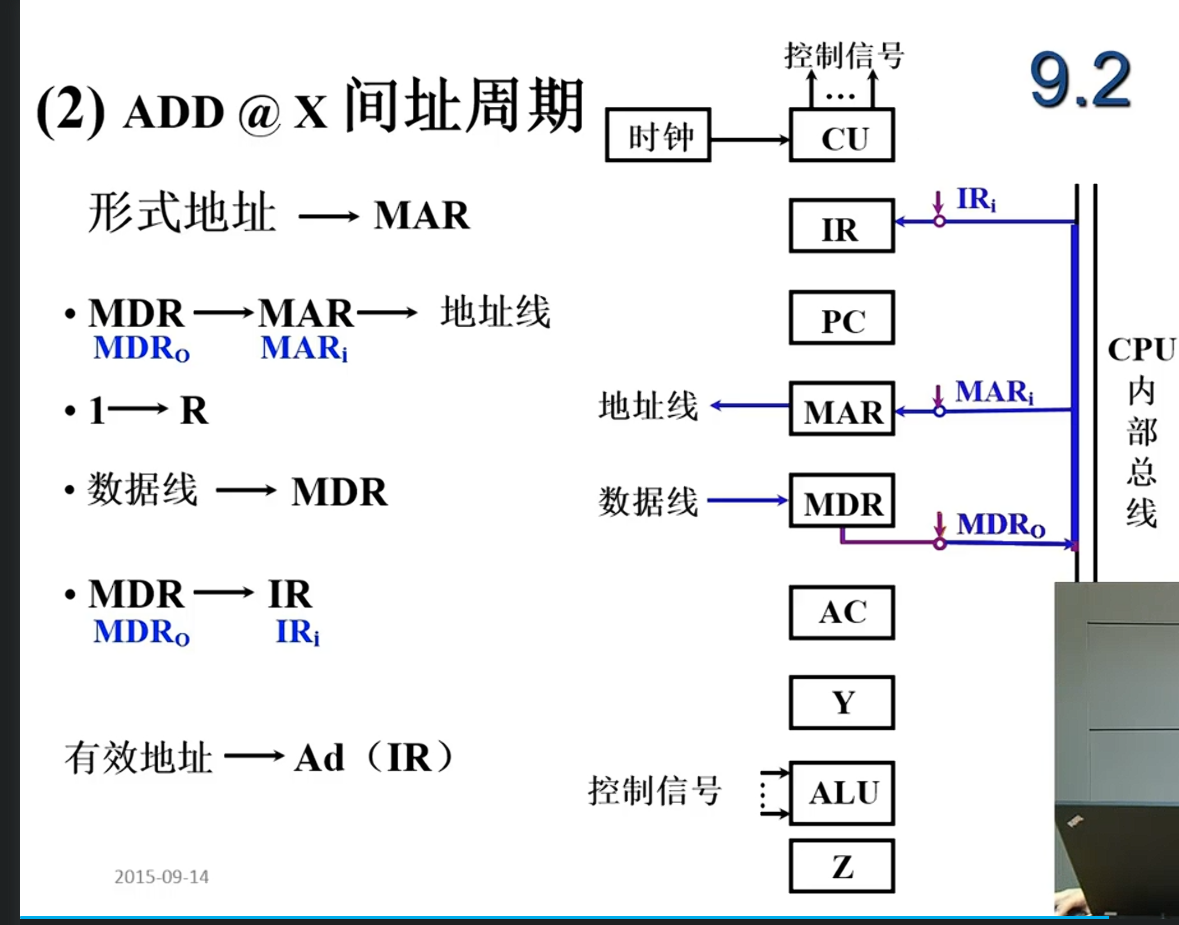
ADD @X
C0: 将PC存储的地址送到MAR
C1: 将MAR的内容送到地址线，发出读命令
C2: 将存储器发回的数据存到MDR
C3: 将MDR保存的指令传到IR
C4: 将IR的操作码部分OP(IR)传到CU,进行译码 取到指令之后寻址特征位发挥作用，如果让IND触发器置1，那么就变成要进入间址周期
C5: 将MDR中保存的形式地址A传到MAR Ad(IR)-> MAR
C1 C2 执行完之后MDR中保存了EA
C3 : EA->OP(IR)
C5: MDR中地址EA传到MAR
C1 C2 执行完之后MDR中保存了数据X
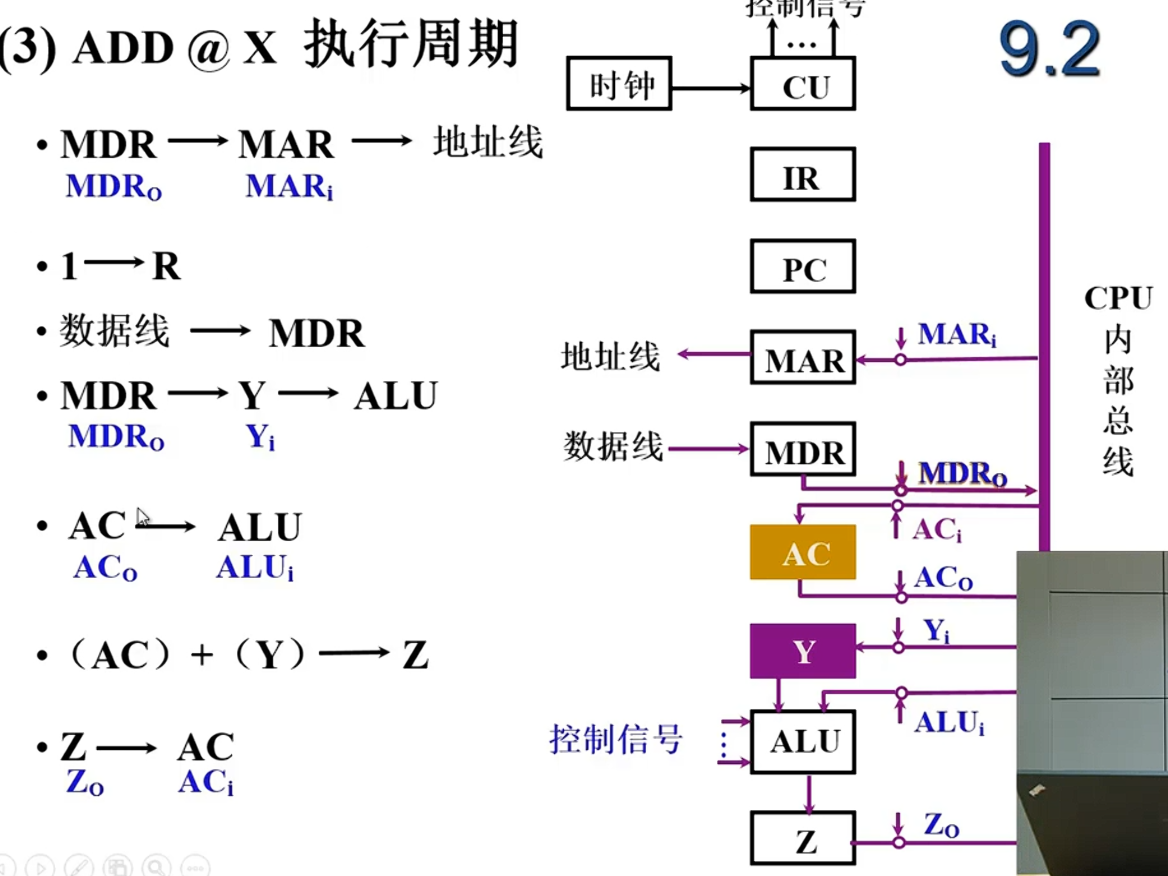
C6C7: 两个操作数x和acc分别送到ALU中，ALU再接收来自CU的加法信号
C8: ALU的运算结果保存到ACC中
采用总线
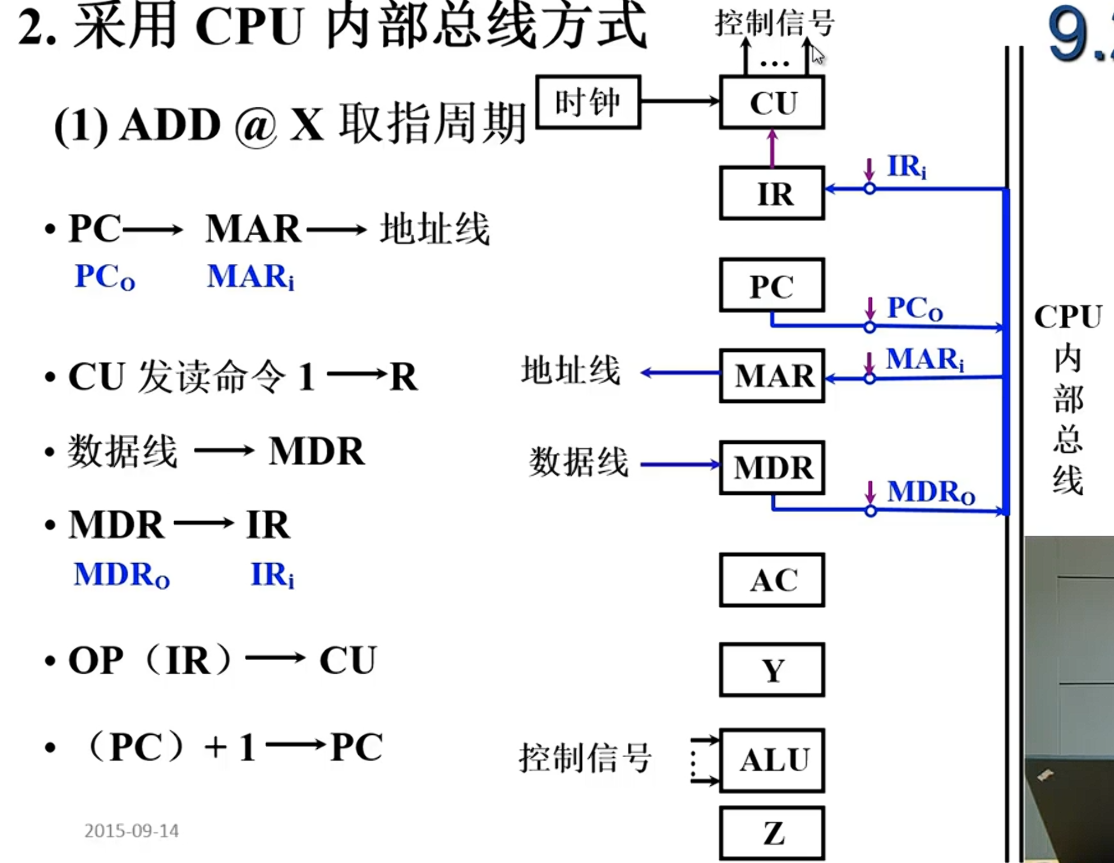
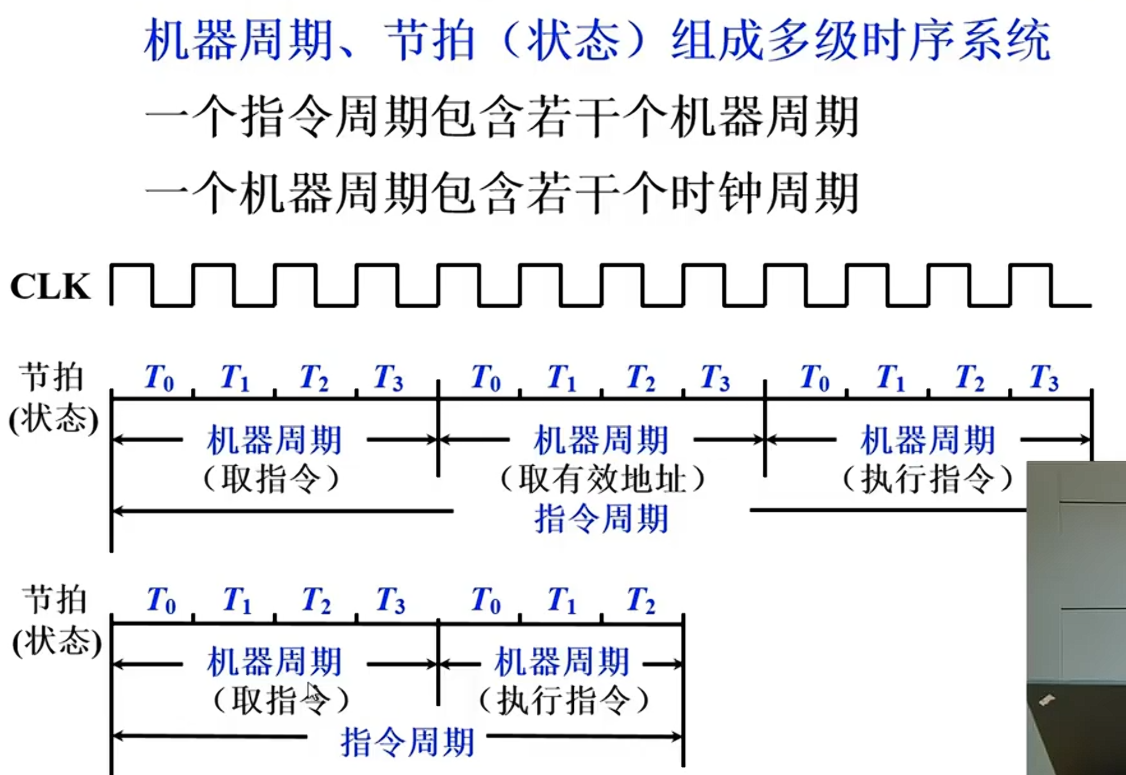
多级时序系统
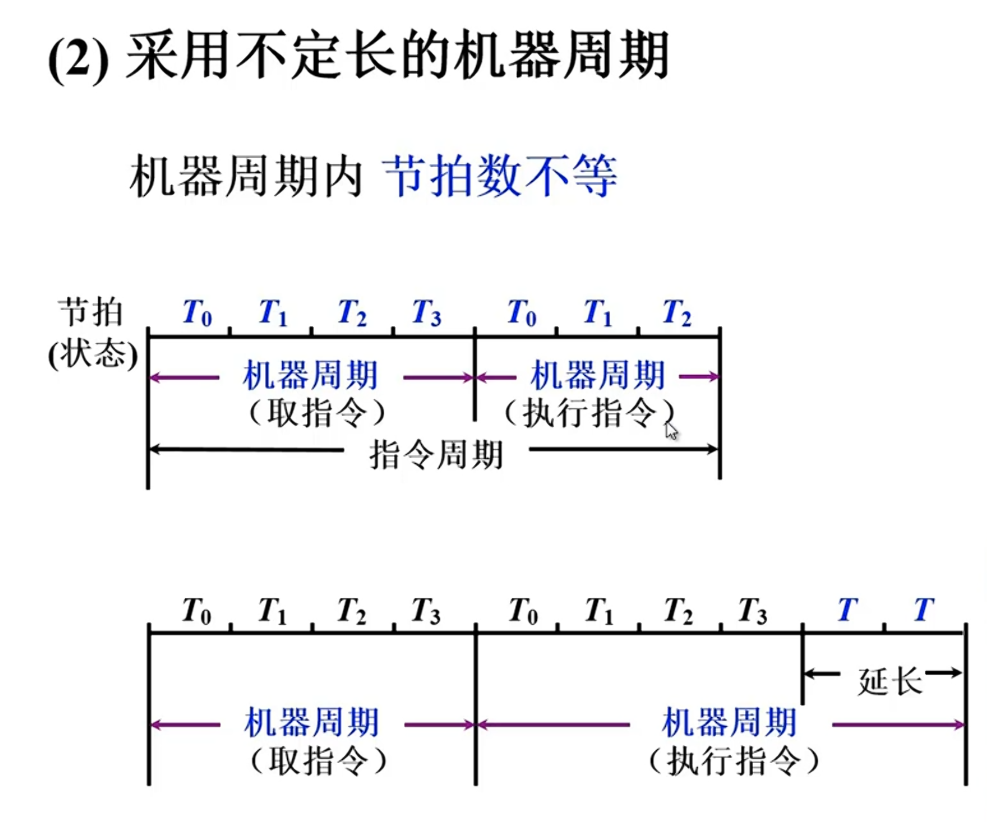
机器周期
定义：所有指令执行过程的一个基准时间
因素：指令的执行步骤，步骤花费的时间
基准：以完成最复杂指令功能的时间为准，以访问一次存储器的时间为基准
指令字长=存储字长 -> 取指周期=机器周期
时钟周期
一个机器周期完成若干微操作，等分为若干个时钟周期，一个时钟周期能够产生一个或多个(并行)的微操作。最小的时间单位
多级时序
主频和速度的关系
流水线同样能加快速度
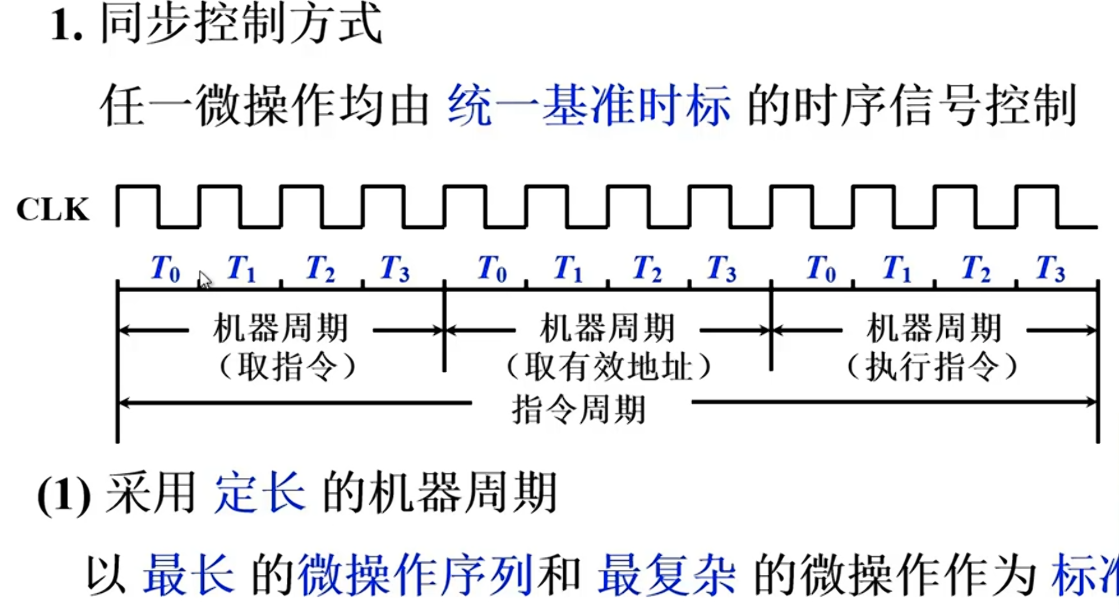
控制方式
产生微操作命令序列的时序控制方式
控制器
硬布线控制器
用复杂的组合逻辑门电路和一些触发器构成
在列出微操作时间表后，综合分析之后，可以将微操作信号的逻辑表达式写出来，
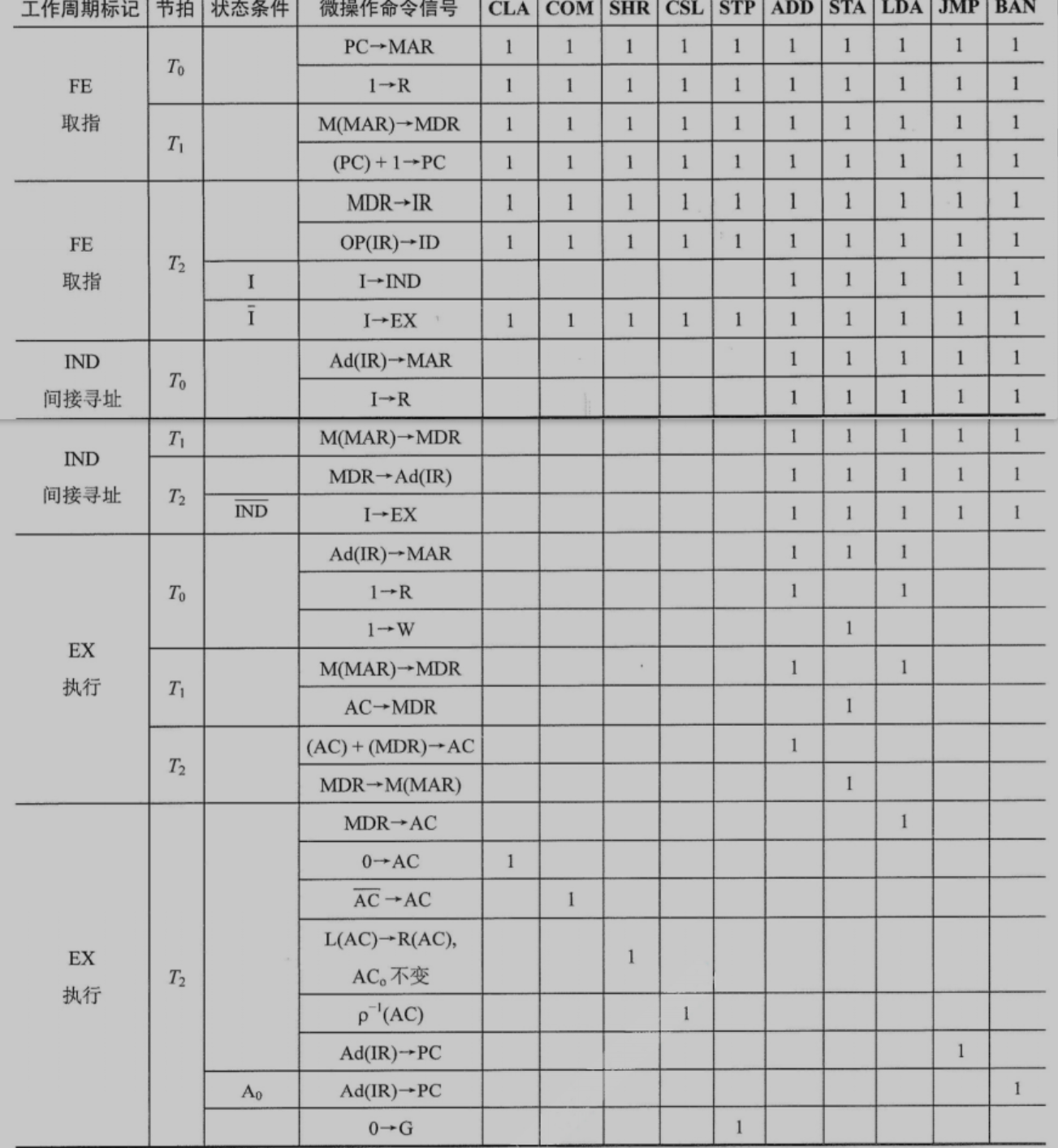
微程序控制器
微操作是计算机中最小的不可再分的操作，微命令作为微操作的控制信号，微命令之间有相容和相斥两种关系，微命令组成微指令，微指令组成微程序，一条机器指令转化成一个微程序并存入一个专门的存储器，微程序控制器通过取微程序存储器中的微指令并执行
微指令编码方式：直接编码、字段直接编码、字段间接编码
