离散数学:群环域
群、环、域
特殊元
幂等元:$a^2=e$
单位元:$ax=x$
零元:$ax=a$
逆元:$ab=e$
群的概念递进
广群:封闭
半群:封闭+可结合
独异点:封闭+可结合+有单位元
群:封闭+可结合+有单位元+所有元素有逆元
阿贝尔群:群+可交换
环、域的概念递进
环:$(R,+,*)$ +是阿贝尔群,*是半群,并且*对+满足分配律
域:$(F,+,*)$ 是一个乘法含有单位元的环,并且F扣去零之后就是乘法的阿贝尔群(整环 + 非零元都可逆。)
整环:单位交换环,和域的区别是少了逆元(环 + 无零因子 + 交换 + 单位元。)
群的阶、元素的阶
群的阶:里面有n个元素即为n阶群
元素的阶:存在最小正整数k使得 $a^k=e$,那么a就为k阶元。
- 一阶元:$a=e$,只有一个一阶元
- 二阶元:$a^2=e$,因此 $a=a^{-1}$,a和其逆元实际上是一个元素。
- 二阶元以上:$a≠a^{-1}$,所以a和其逆元成对出现。
- 推论:偶数阶的群,一定含有二阶元:二阶以上成对出现,一阶元只有一个,那么必定存在二阶元。
子群、拉格朗日定理
平凡群:只有一个元素(单位元)是所有群的子群,同时也是循环群、阿贝尔群。
子群证明:
- H是G非空子集。H通常是加了条件限定的,代入单位元证明其非空
- H对于运算是封闭的。H的元素同样也是G的元素,同样具备G的特性,利用G的特性,证明H的元素符合之前的条件限定。逆元可以使用 $xy^{-1}$进行变换。
- H的非零元素都存在逆元
求所有子群:
- 阶为1的子群:单位元
- 阶为2的子群:单位元、平方等于单位元的元素。。。。
- 阶为4的子群:单位元、四次放等于单位元的元素。。。。。
拉格朗日定理:对于有限群 G 和其子群 H,H 阶 必然是 G阶 的因子。陪集数量乘H阶=G阶
- G的元素a,a 阶k 必然是 G阶n 的因子,并且 $a^n=e$(并不代表a是n阶元,因为n是k的倍数)
- 若 ∣G∣= n,则 G 的子群的阶只能是 n 的约数。
- 6-> 子群阶只能是1,2,3,6
- 8-> 1,2,4,8
- 左右陪集阶为 H阶,左右陪集要么相同,要么不相交
- H,K为子群,H交K就是H,K的子集,所以H交K是 H 和 K 的因子,其能够整除HK的最大公因数。因为HK互质,所以 H交K只能是一阶
循环群
循环群:G中存在一个元素a,使得所有的元素都可以表达为 a 的幂次方的形式,那么a是群的生成元,G是循环群
循环群的性质:
- n 阶循环群,生成元也是 n阶元,即 $g^n=e$
- 一定是阿贝尔群
- n 阶循环群,同构于$(N_n, +_n)$
- 无限循环群,同构于$(I_n,+_n)$
群的性质总结
群的性质:
- 逆元和单位元唯一,没有零元
- $(a\times b)^{-1}=b^{-1}\times a^{-1}$ 重要,证明题里面逆元出现
- 支持左右消去 ,方程一定可解
- 每个元素在运算表的行/列必然出现且只会出现一次
- 阶的性质
- 素数阶群必是循环群,没有非平凡子群,并且除了单位元,剩下的全都是生成元。
- 逆元和自己有着相同的阶数
群的同态
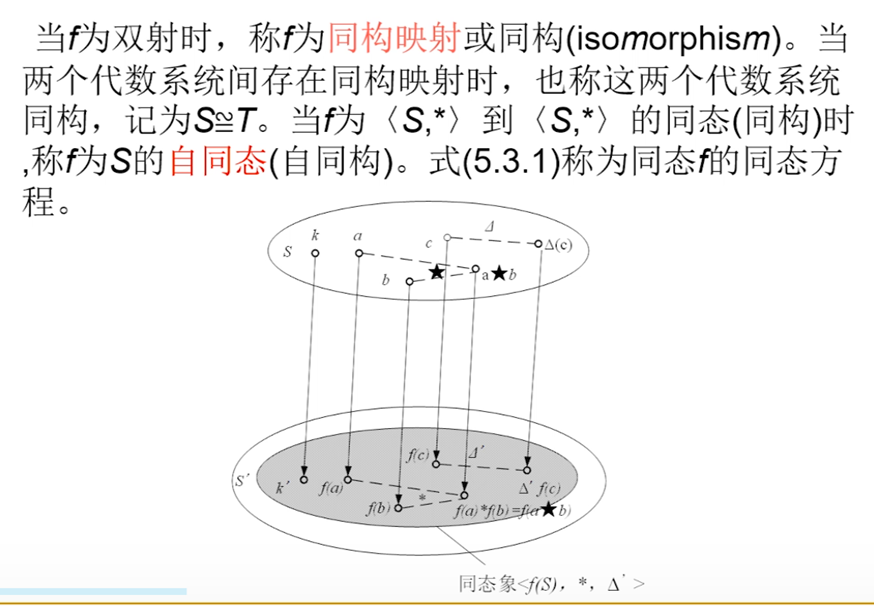
群的同态和同构:
同态: $f(a*b) = f(a)+f(b)$ 如果是$f(ab)=f(a)f(b)$,那就是自同态。
同构:f是双射的同态
同态核K:S中那些经过映射之后变成 S’单位元的元素,如果只有S的单位元,说明是单射
f(e) = e
证明题:对于 x∈K,f(x)=e,
证明自同构:
- f是双射
- 先证明是入射: 任取不相等的两个元素x1x2,f(x1) f(x2)肯定不相等
- 再证明满射: 对于任意一个y,肯定有一个x∈G对应
- f(xy)=f(x)f(y)