离散数学：格
格及其判定
偏序集 (P, ≤)
- 反身性：∀a∈P, a≤a
- 反对称：a≤b且b≤a ⇒ a=b
- 传递性：a≤b且b≤c ⇒ a≤c
格 (L, ∧, ∨)
- 定义：对任意a,b∈L, 最小上界a∨b和最大下界a∧b均存在
- 最小上界：满足大于等于他们俩的最近的一个元素
- 最大下界：满足小于等于他们俩的最近的一个元素
- 等价公理：交换律、结合律、吸收律
- 如图右下角 ，e和f之间没有最小上界，因此不是格
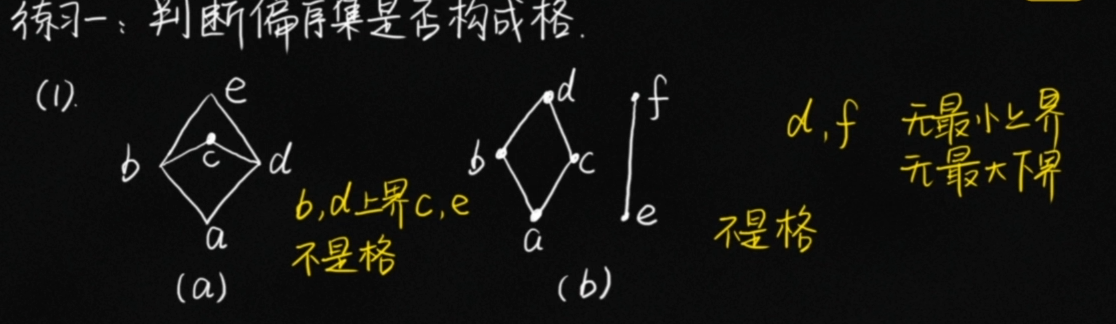
- ec无法找出。df无法找出
- 幂集（所有子集构成的集合）上的包含关系是格
格的判定技巧：最底层/最上层的两个元素之间完全没关系因此不可比较。存在多个上界或者多个下界。
子格、格同态
子格
- H⊆L, 若(H,∨,∧)满足格的封闭性和公理，即为子格
- 格L的非空子集S构成L的子格的条件：H对L的∨,∧运算封闭。 在原格中做运算的结果还在 H里面，那么就是封闭的
- 分配性可以继承，但是有补性不一定（有补性跟元素相关，少了一个元素可能就没有对应的补元了）
格同态
- 存在双射f:L→M, 满足f(a∨b)=f(a)∨f(b), f(a∧b)=f(a)∧f(b)
有补格
有界格：格(L, ∧, ∨,O,I)
- 格的全上界：对任意元素x，这个元素I都满足x<=I
- 格的全下界：对任意元素x，这个元素O都满足b<=O
元素a的补元：有界格中，如果存在 b∈L，使得a和b的最大下界是0（全下界），a和b的最小上界是1（全上界）那么b为a的补元。因此8和1互为补元，24没有补元
要么是全上界和全下界互为补元，要么是中间平行的这几个互为补元。
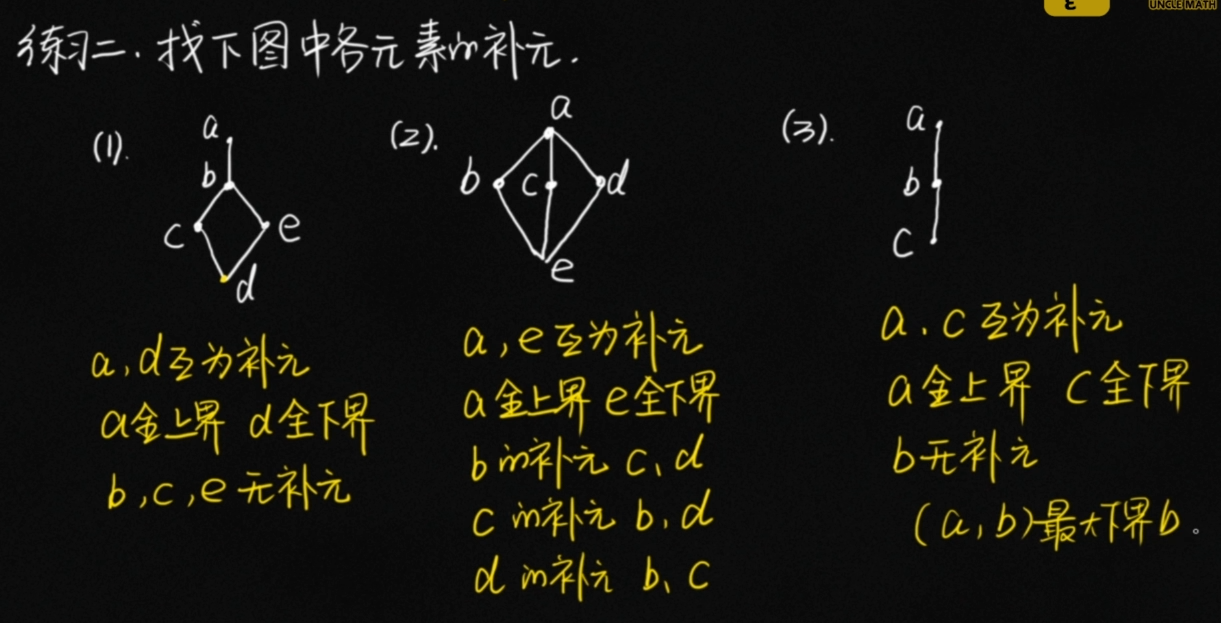
有补格：每个元素都有至少一个补元。
分配格
分配格：格的 ∧, ∨满足分配律。链、密集、命题格都是分配格
- 判别：不存在钻石格或者五角格同构的子格
- 四个元素及以下的都是分配格
- 五个元素，除了五角格和钻石格，其他都是分配格
- 性质：支持消去律
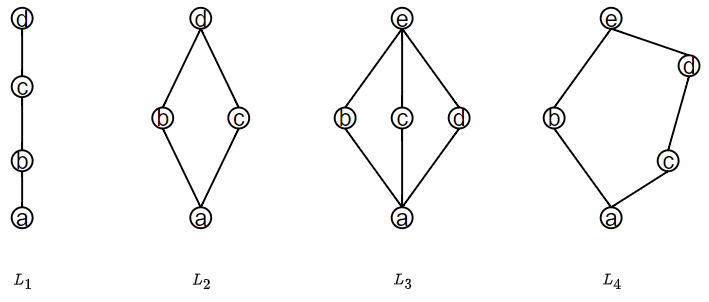L1,L2L1,L2是分配格， L3(钻石格),L4(五角格)L3(钻石格),L4(五角格)不是分配格。
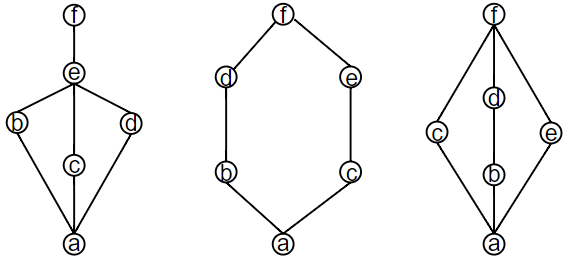上述都不是分配格。 它们是钻石格或五角格的子格。
布尔代数
布尔代数（布尔格）：如果有补格的∧, ∨满足分配律，那么他就是一个布尔格（布尔代数）每个元素有且只有唯一的一个补元
（2）两个元素的最小上界是全下界0，那么他们都是0。 由此可知 a和b’互为补元 b就是a
性质：
双重性：任何布尔恒等式对偶仍成立
Stone表征定理：每个布尔代数同构于某个集合代数的幂集（P(X), ∪, ∩, ᶜ）
模格
- x∨(y∧z)=(x∨y)∧z
- 所有分配格都是模格，反过来不一定。
对偶格：把一个格中的“$\vee$”和“$\wedge$”运算、以及“$\leq$”和“$\geq$”关系全部反向，得到的新格。它是从原格“逆向”得到的结构。
题
- 判定题：给出下列偏序集，判断是否构成格，并说明理由。
a. (所有自然数N, 整除关系) b. (P({1,2,3}), ⊆) - 等式证明：在任意格中证明：
a. (a∨b)∧(a∨c) = a∨(b∧c)
b. a∧(b∨c) ≥ (a∧b)∨(a∧c) - 子格判别：设L是格，H={x∈L | x≥a}，证明H是L的子格
- 特殊格判别：给定有界格, 判断其是否为：
a. 分配格 b. 补格 c. 布尔格 - 有限布尔代数：列出所有阶为4的布尔代数，并验证它们满足补元律
- 判定题：
a. (N,|) 的上确界 gcd(m,n) 存在，下确界 lcm(m,n) 存在 ⇒ 是格
b. (P(X),⊆) 的∧=交集、∨=并集 ⇒ 是格 - 等式证明：
a. 左边 = (a∨b)∧(a∨c) = a∨(b∧c) （分配律）
b. 由吸收律和分配可得 ≥ 方向 - 子格判别：
- H封闭：若x,y≥a，则x∨y≥a, x∧y≥a
- 满足格公理
- 特殊格判别：
- 分配：验证分配律是否在格中成立
- 补格：对每个元素检查是否存在补元
- 布尔格：同时满足上述两条
- 阶4布尔代数：
- 同构于P({1,2})，元素{∅,{1},{2},{1,2}}，补元为集合补集