离散数学:图、树
图的基本概念
概念介绍
平凡图:只有一个定点,没有任何边。
无向图

v4 悬挂节点 只有一个边e4
e4 悬挂边
有向图
平行边必须起点终点都相同,引入了出入度的概念

握手定理(节点个数和边的关系)
- 节点数n,边数e,所有n个节点的入度出度之和 = 2e(偶数)(计算题)
- 推论:任何图中,度数为奇数的节点个数必为偶数(判定是否能作为图的节点的度数序列)
- 推论:有向图中,所有节点的出度之和=所有节点的入度之和=e
n 阶 无向简单图: 有n个节点,不含平行边,不含环
PS:如果n阶无向简单图中,有p个n-1度的节点,说明其他节点的度数最小就是p,不可能存在比p小的度数(7阶简单图,6,6,5,4,3,3,1)
通路、回路、连通
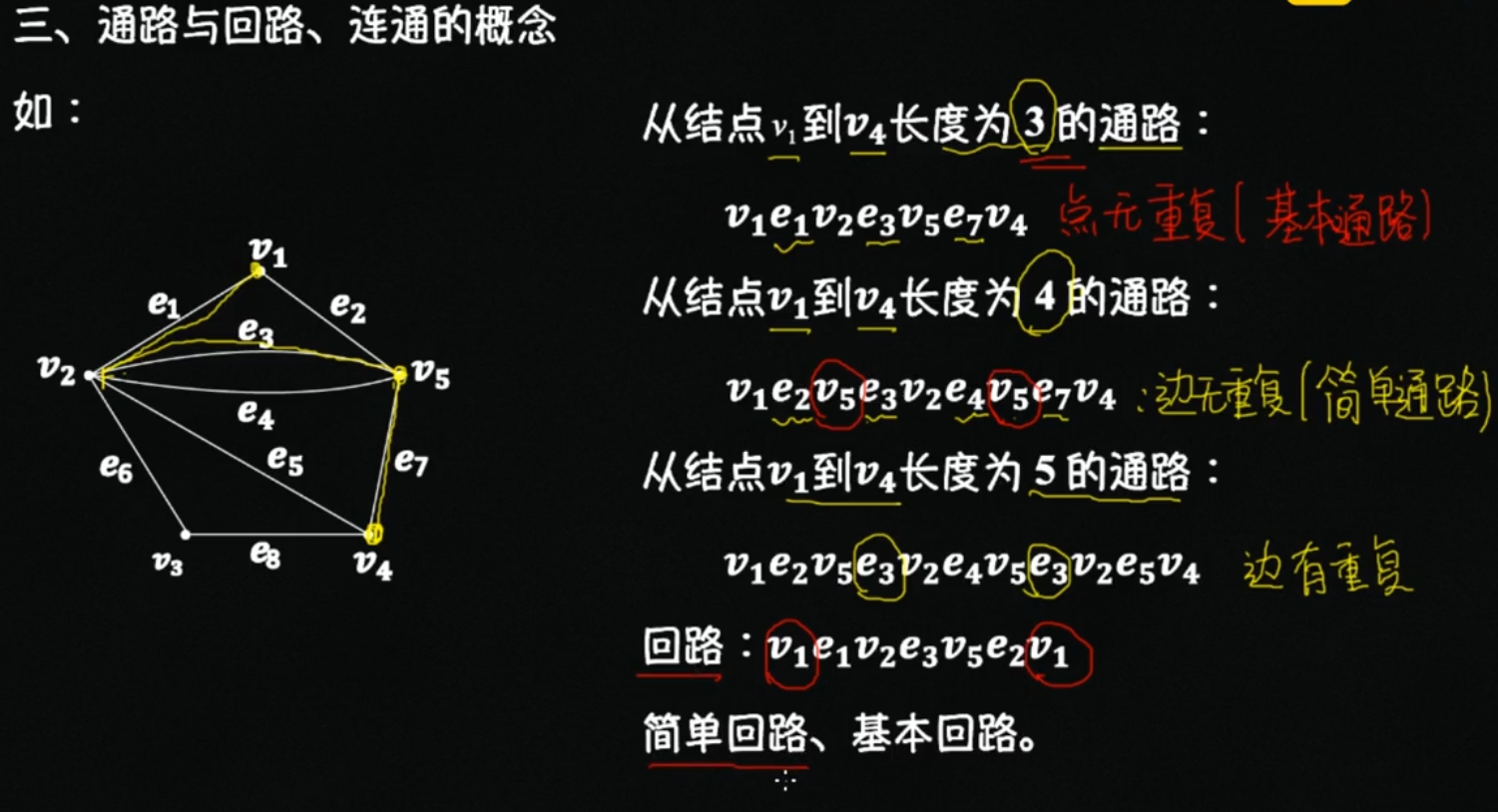
基本通路:点不重复、边也不重
简单通路:边不重复
回路:起点等于终点的通路
连通图:
- 无向连通图G:任意两节点之间都有一条通路,则G为 无向连通图
- 有向连通图G(V,E):任意两节点uv,u到v存在通路则u到v可达,否则称u到v不可达。推之,可有相互可达的推论,一个节点到自己总是可达的
- G中任意两个节点,至少从一个节点到另一个节点是可达的,则G 单向连通
- G中任意两个节点之间均为互相可达,则G 强连通
- G中在略去方向之后得到的无向图连通,则G 弱连通
- 任意一种连通都可以叫做 有向连通图
邻接矩阵计算通路数目
邻接矩阵A:顶点作为坐标轴,数字就填直接连接的边数目。

- A: Aij 就是vi到vj长度为1的通路条数。
- A的n次:Aij 就是vi到vj长度为n的通路条数。
- 起点终点一样的通路就是回路
可达矩阵
可达矩阵P:数字填写两顶点之间是否可达,若可达则1,反之0
是否可达:先看A4,A4里面只要是正的那就是可达,如果出现了0,就翻回去看看A3 A2 A1,如果全是0,那么才是不可达的

关联矩阵

欧拉图、哈密顿图
概念
欧拉图
欧拉通路:通过G中所有边 一次且仅一次的通路
欧拉回路:欧拉通路(起点和中点相同)
欧拉图:有欧拉回路的图
半欧拉图:只有有欧拉通路的图
推论:欧拉图度数均为偶数,半欧拉图有且只有两个奇度节点
无向连通图是欧拉图:所有节点度数均为偶数
无向连通图是半欧拉图:只有两个奇度节点
有向连通图是欧拉图:每个节点的入度=出度(度数为偶数)
有向连通图是半欧拉图:只有两个奇度节点,其中一个节点的入度比出度大1,另一个的出度比入度大1。其余每个节点的入度=出度
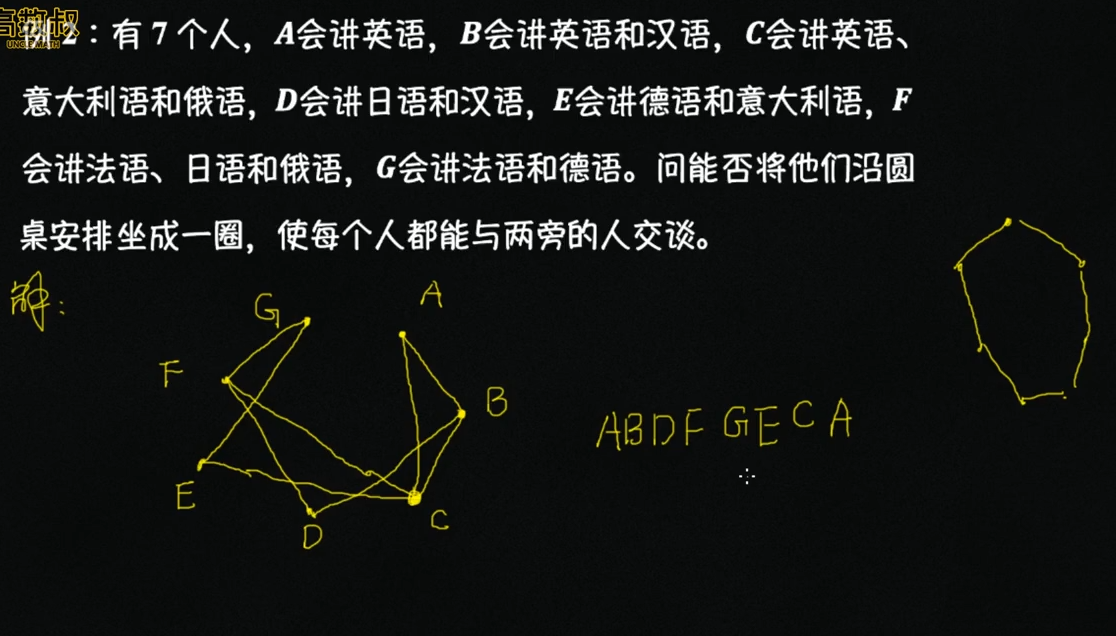
哈密顿图(设计题)
哈密顿回路:G中一条包含所有节点一次且进一次的回路。图G为哈密顿图
哈密顿通路:G中一条包含所有节点一次且进一次的通路。只有这个,图G为半哈密顿图
最短路问题(Dijkstra 标号法)
树
树的定义
任意两顶点之间存在唯一路径
G无回路/连通 且节点数=边数+1

N阶非平凡的无向树至少有两片树叶
握手定理
节点数 = 边数 + 1
度数 = 边数 * 2

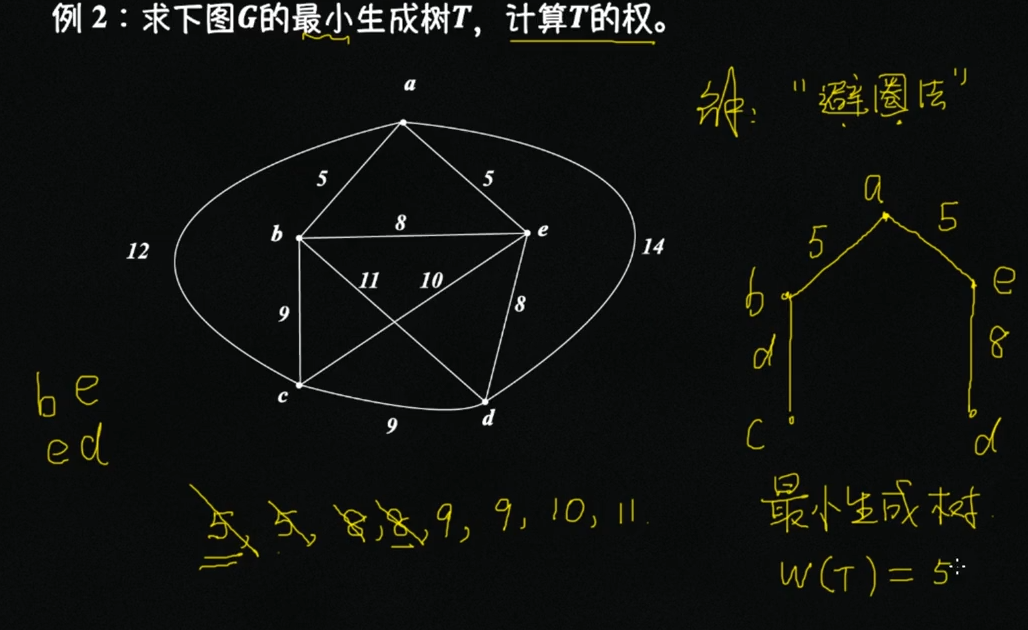
最小生成树(求连通图的最小权的生成树)
连通图G中的所有生成树中,带权最小的生成树 就是最小生成树。最后形成树,顶点比边多一条
避圈法(添加的时候不要形成圈)
边按照权从小到大排列,逐次连线,注意不要形成圈
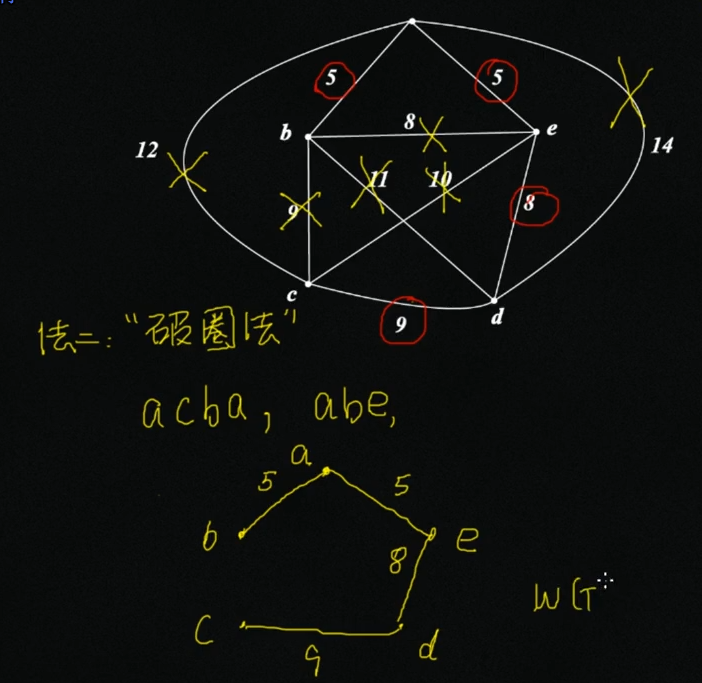
破圈法(见圈就破)
找圈,去掉其中权最大的那条边
根树
有向树:如果有向图的基是一个无向树,那么这个有向图就是有向树
根树:一个顶点入度为0,其余的入度为1的有向树。这个顶点是树根
层数:根到顶点的长度

v1 是树的树根,v1到v2是一条有向边。v1 是v5可达,那么v1就是v5祖先,反过来v5是v1后代。最多分几叉就是几叉树
最优二元树(哈夫曼树)
求带权 3,4,5,8,9 的最优二元树(除了树叶,其他所有的分支节点的度数都为2 )3,4,5,8,9
首先,34合并为7。第二步,57合并为12。第三部,89合并为17。最后一步,12 17合并为29
其他树概念
完全二叉树:边数=2x-2 x为叶子数
平面图
设计电路,线路不能交叉。除了顶点之外的任意两条边都不相交。
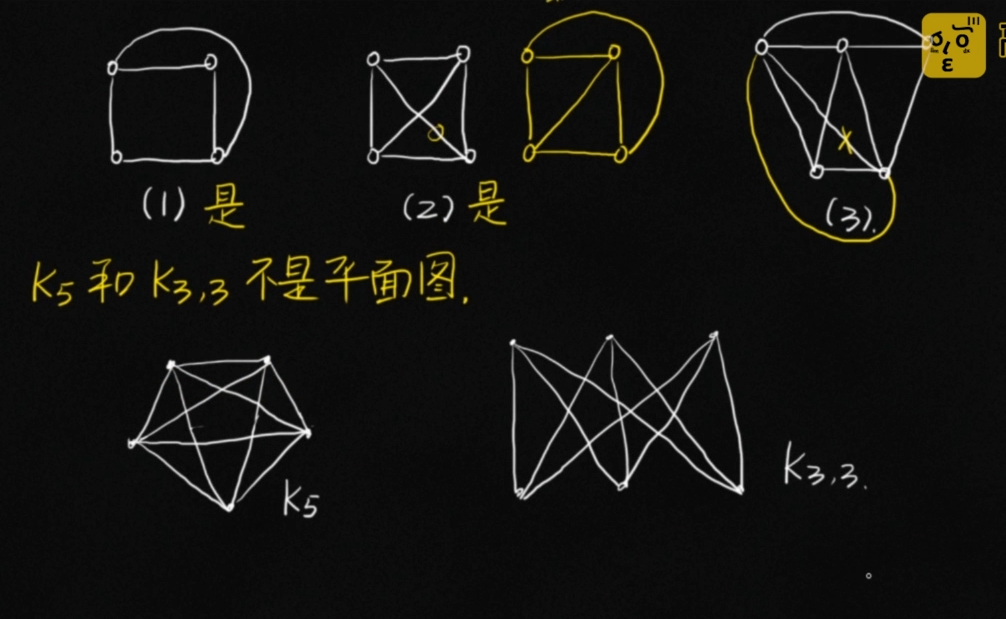
平面图满足欧拉公式
次数:面的边界所包含的边数
平面图所有面的次数之和 = 2e (边数的2倍)一条边提供两个次数
- 欧拉公式:G为任意连通平面图,n个顶点,m条边,r个面。那么, $n-m+r=2$
- 推广:G为任意平面图,有k个连通分支(k>=2)。那么, $n-m+r=k+1$
对偶图
G是简单图,每个面指定一个新的节点,只要是两面的一条公共边就让节点连一条边与其相交。新的点和边组成的图就是图G的对偶图。
对偶图的边数m’和原来相同,顶点数n’和原来的面数r相同
结论:平面图的对偶图一定是平面图,一定满足欧拉公式
边e是环,对应到对偶图里面就是桥,反之一样。
着色
二部图
判定定理: